16.5. Интегрирование рациональных дробей с квадратным трехчленом в знаменателе
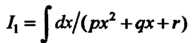
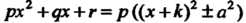
На до полного квадрата по формуле рх+дх + г = р((х + к)±а) сводится к одному из двух интегралов:
Ли 1 и _
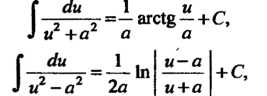
~2=— агс1§ —+С,
(16.15)
(16.16)
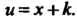
Где и = х + к. Интеграл
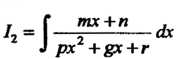
1 I ¦> I
= — 1п и +а +С.
(16.17)
Рх +&С+Г
Сводится к интегралу (16.15) или (16.16) и интегралу
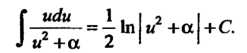
(16.18)
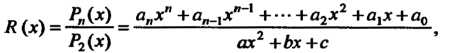
Сначала производят деление; в результате получают К(х)=()т(х)+ (кх+1)/(ах?+Ьх+с), где <2т(х) - многочлен, степень которого ниже степени многочлена Р„(х).
П,„, рЛх) а„х" +ап-1х" + —+а2* +а, х + а0 ' ' п { \ 2 г 9
”2С*) сгх +Ьх+С
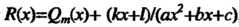
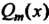
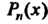
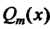
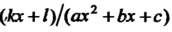
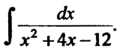
ЕЬс
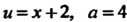
Пример 16.18. Найти интеграл
Дополняя квадратный трехчлен до полного квадрата и интегрируя на основании формулы (16.16) для случая, когда и—х+2, а-4, находим
Первообразная от многочлена (2т(х) находится непосредственно, а от остатка
(,кх+1)/(ах2 +Ьх +с) - как интеграл ввда (16.17).
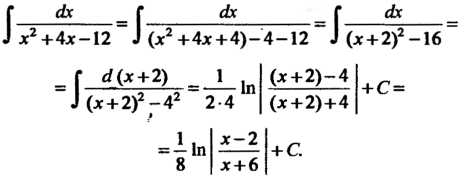
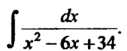
} х2 -6х +34
Выделяя полный квадрат и применяя формулу (16.15) для случая, когда и = х-3, а = 5, находим
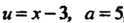
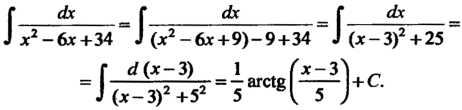
Г Ах__Г_Ах__ Г (1х __
^ х2 - 6х + 34 .1 (х2 -6х+9)-9+34 (х-3)2 + 25~ г а(х-3) 1 ^
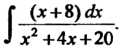
Пример 16.20. Найти Г + .
•1х2+4х+20
Преобразуя подынтегральное выражение, получаем
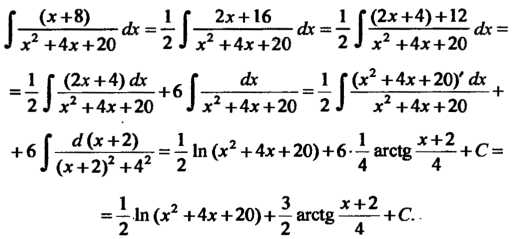
Г 2(^8)......*лГ-^±16_а,1 г&±а±ил=
•> х +4х + 20 2 ^ х +4х+20 2^2+4х + 20
_ 1 Г (2х+4)<& Г Л _ 1 Г (х2 +4х + 20)' Ах | 2^2+4х+20 Зх2+4х+20 2^ х2+4х + 20
+ 6 Г ^ ^ 2 = — 1п (х2 + 4-у + 20)+6 ¦ -1- агс{{> * +- + С =
= — 1п (х2 +4х+20)+— агс1}> +С.
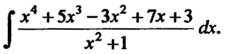
П 1*01 и Гх4+5х3-3х2+7х + 3 ,
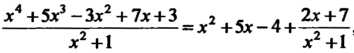
Гх4+5х3-3х2 + 7х + 3 , х3 5 2 . ,, 2 п * . ^
I-,-<1х = —+—х -4х + 1п(х +1)+7агс*8* + С.
.1 х +1 3 2
„ х4+5х3-Зх2+ 7х+3 2 , 2х + 7
| < Предыдущая | Следующая > |
|---|