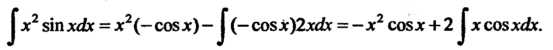16.4. Метод интегрирования по частям

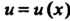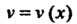ЕслиI,- дифференцируемые функции от.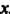, то из формулы

Для дифференциала произведения двух функций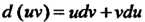Получается

Формула интегрирования по частям

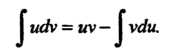
(16.12)

Эта формула применяется в случае, когда подынтегральная функция представляет собой произведение алгебраической и трансцендентной функций. В качестве 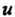Обычно выбирается функция, которая упрощается дифференцированием, в качестве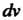— оставшаяся часть подынтегрального выражения, содержащая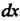, из которой можно определить V путем интегрирования.

В некоторых случаях для сведения данного интеграла к одной из формул простейших интегралов формула (16.12) применяется несколько раз. Иногда искомый интеграл определяется из алгебраического уравнения, получающегося с помощью интегрирования по частям.

Пример 16.11. Найти интеграл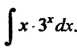

Полагаем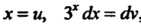, откуда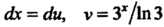(по формуле 4 про

Стейших интегралов). Подставляя эти выражения в формулу (16.12), получаем

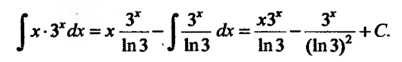
Замечание. Результат можно проверить дифференцированием:

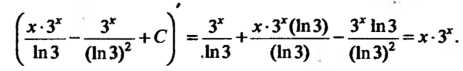
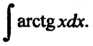
Пример 16.12. Найти интеграл

Полагая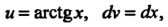Находим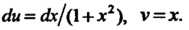

По формуле (16.12) получаем

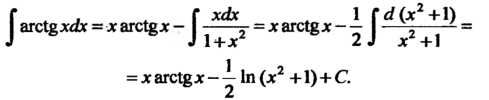
Пример 16.13. Найти интеграл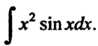

Полагая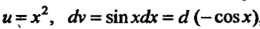, получаем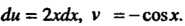

Следовательно,

(I)

Полученный интеграл снова находится интегрированием по частям. Его можно найти и не вводя явно функци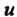иИ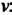

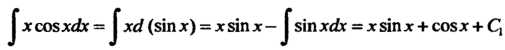
Подставляя эта выражение для интеграла в формулу (I), находим

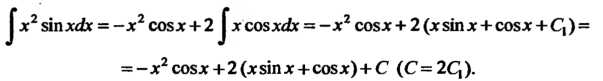
Пример 16.14. Найти интеграл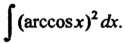

Полагая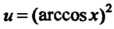,,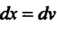 получаем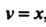

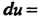
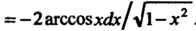. По формуле (16.12) имеем

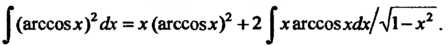
Этот интеграл также находим методом интегрирования по частям:

266

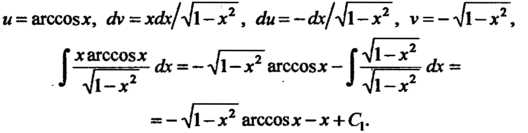
Следовательно,

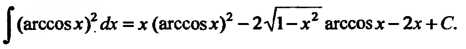
Пример 16.15. Найти интеграл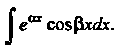

Полагая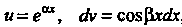, находим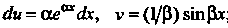; следо

Вательно,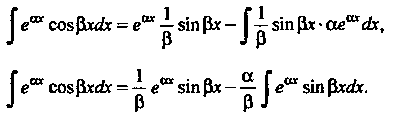

Интеграл в правой части равенства (I) также находим методом интегрирования по частям:

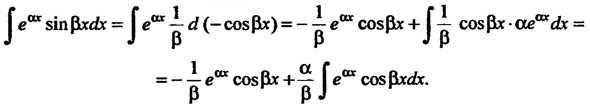
(II)

Подставив выражение (II) в равенство (I), получим 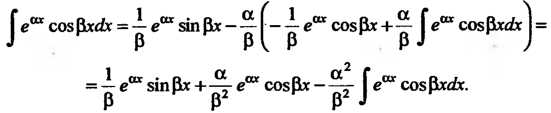 Перенося интеграл в левую часть, получаем уравнение

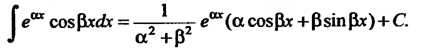
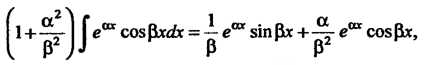
Пример 16.16. Найти интеграл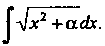

Положим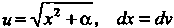, отсюда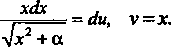По формуле

(16.12) получаем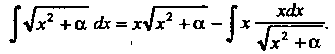

Преобразуем интеграл в правой части

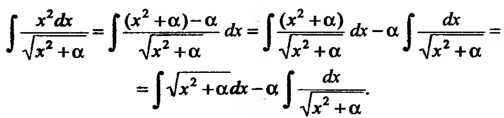
Следовательно,

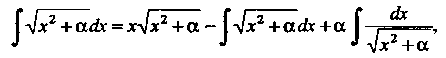
Откуда

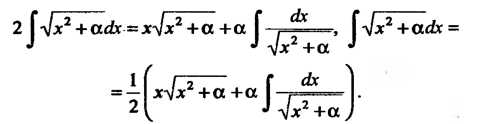
Так как последний интеграл определяется формулой (16.11), то

(16.13)

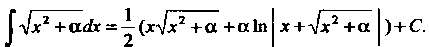
Пример 16.17. Найти интеграл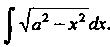 Применяя метод интегрирования по частям, получаем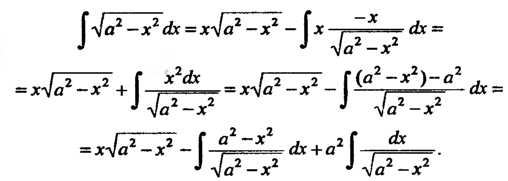

Поскольку

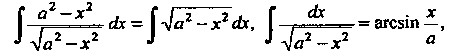
То

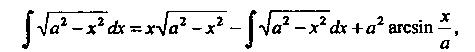
Откуда

(16.14)

Помощью

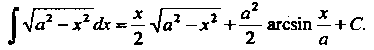
Замечание. Этот интеграл можно найти с подстановки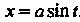

< Предыдущая		Следующая >