16.3. Метод подстановки

Интегрирование путем введения новой переменной (метод подстановки) основано на формуле

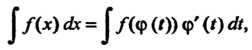(16.10)

Где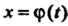- дифференцируемая функция переменой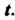

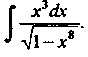
По формуле

Откуда

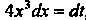
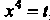
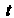
Введем новую переменнук

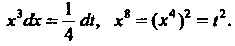
П р и м е р 16.9. Найти интеграл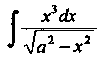

В случае, когда подынтегральное выражение содержит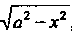, целесооб

Разно применить тригонометрическую подстановку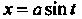Или

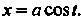
Положим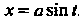, тогда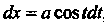, поэтому

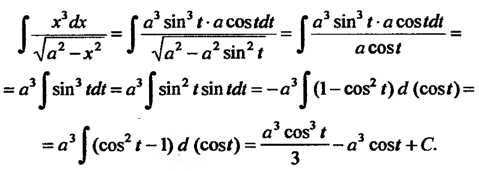
Заметив, что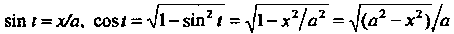, получим

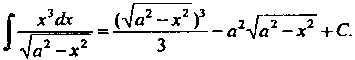
Переходя к новой переменной и используя формулу 10 простейших интегралов, получаем

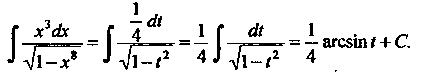
Возвращаясь к переменной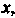Находим

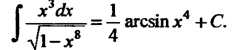
Замечание. Результат можно проверить дифференцированием. Так как

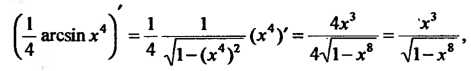
То на основании формулы (16.4) заключаем, что пример решен верно.

Пример 16.10. Найти интеграл’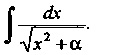

Применим так называемую подстановку Эйлера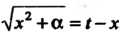, где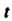-новая

Переменная. Переписав это равенство в виде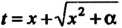И взяв дифференциа

Лы от его обеих частей, получим

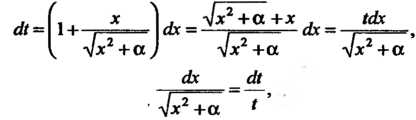
Откуда

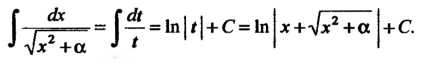
(16.11)

Итак,

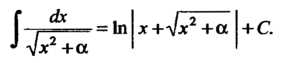
< Предыдущая		Следующая >