16.2. Непосредственное интегрирование

Непосредственное интегрирование основано на свойстве 4 неопределенного интеграла

Бели функции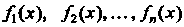Имеют первообразные в некотором про

Межутке, то функция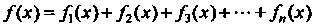Также имеет перво

Образную в том же промежутке, причем

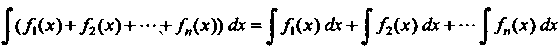, (16.9)

Т. е. неопределенный интеграл от алгебраической суммы конечного числа функций равен такой же алгебраической сумме неопределенных интегралов от слагаемых.

Пример 16.1. Найти неопределенный интеграл

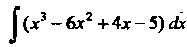
Пользуясь свойствами неопределенного интеграла, формулой (16.9) и первыми двумя формулами простейших неопределенных интегралов, находим

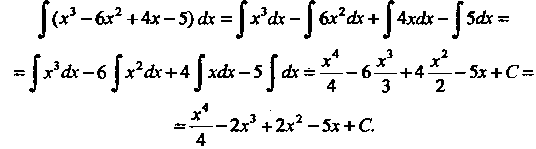
Замечание. Постоянное слагаемое не записано при нахождении каждого интеграла алгебраической суммы, а лишь один раз, так как сумма произвольных постоянных величин есть величина постоянная.

Пример 16.2. Найти интеграл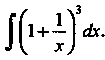

Преобразуя подынтегральную функцию и пользуясь первыми тремя формулами неопределенных интегралов, получаем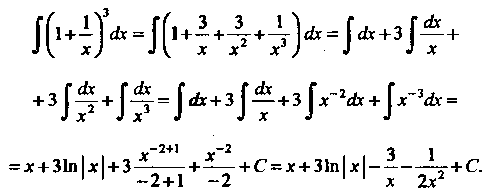

Пример 16.3. Найти неопределенный интеграл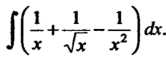 С помощью формул 2 и 3 простейших интеграле» (при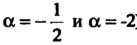) получаем

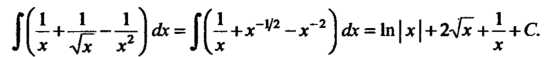
Пример 16.4. Найти интеграл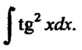

Преобразуя подынтегральную функцию и пользуясь формулами интегралов 1 и 8, находим

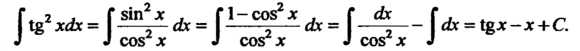
Пример 16.5. Найти интеграл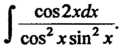 Преобразуя подынтегральную функцию и пользуясь формулами 9, 8, получаем

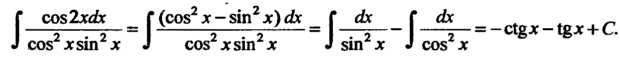
Пример 16.6. Найти интеграл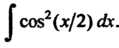 Поскольку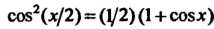, то

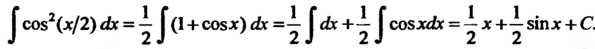
Пример 16.7. Найти интеграл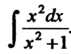

Преобразуя подынтегральную функцию, с помощью формул 1 и И простейших интегралов, находим

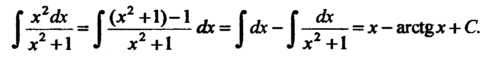
< Предыдущая		Следующая >