16.1. Неопределенный интеграл и его свойства. Таблица основных неопределенных интегралов
Функция Р (дс), определенная в промежутке (а, Ь), называется первообразной данной функции /(дс) в этом промежутке, если для любого значения х е (а, Ь) выполняется равенство
Р'(х) = Дх). (16.1)
Например, функция Р(х) = х5 - первообразная функции /(х) = 5х* в промежутке (-оо, + “), поскольку (х5)' = 5хЛ для всех дс; функция Р(х) = 1пл: - первообразная функции /(лс) = 1/дс в промежутке (0, + °°), так как (1пх)' = 1/х;
Функция Р(дс) = агссозл: — первообразная функции /(х)= = —\]х2 в интервале (-1,1), ибо (агссоклг)' = - \]4\- х2.
Если Р(х) - первообразная функции /(дс), то
Ф (х)=Р(х) + С, (16.2)
Где С - произвольная постоянная, также является ее первообразной.
Выражение (16.2), в котором функция Р(х) удовлетворяет условию (16.1),
Определяет множество всех первообразных данной функции /(дс) в заданном промежутке (а, Ь).
Неопределенным интегралом от данной функции /(*) называется множество всех ее первообразных:
|/(х)е! х = Р(х)+С, (16.3)
Где Р'(х) = /(х). Знак 1 называется знаком неопределенного интеграла, функция /(х) - подынтегральной функцией, выражение /(дс) А -
Подынтегральным выражением.
Операция нахождения первообразной данной функции называется интегрированием.
Неопределенный интеграл обладает следующими основными свойствами.
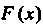
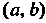
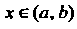
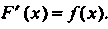
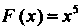
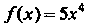
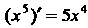
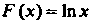
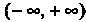
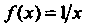
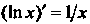
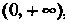
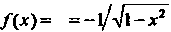
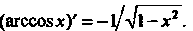
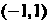
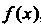
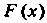
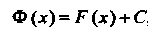
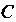
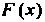
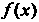
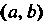
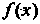
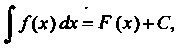
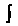
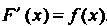
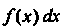
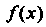
1. Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
(16.4)
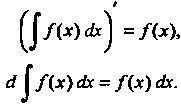 (16.5)
(16.5)
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
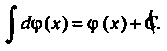 (16.6)
(16.6)
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
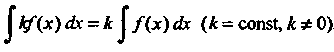 (16.7)
(16.7)
4. Если функции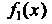 И
И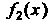 Имеют первообразные, то функция
Имеют первообразные, то функция
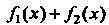 Также имеет первообразную, причем
Также имеет первообразную, причем
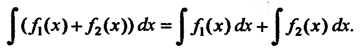 (16.8)
(16.8)
Таблицу простейших неопределенных интегралов нетрудно получить, воспользовавшись тем, что интегрирование является операцией, обратной дифференцированию. Будем исходить из формулы (16.6), которую запишем следующим образом:
Если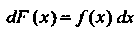 , то
, то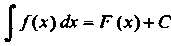 Например, поскольку
Например, поскольку
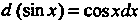 , то
, то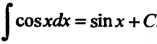
Применяя аналогичное рассуждение к каждой из формул основных дифференциалов (см. п. 14.4), получаем следующие простейшие неопределенные интегралы: 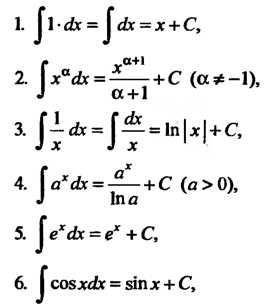
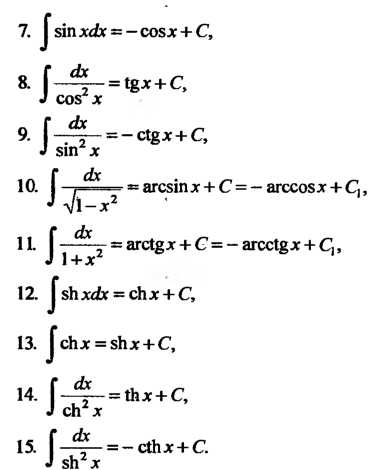
Отметим, что все указанные формулы справедливы в тех промежутках, в которых определены соответствующие функции. Например, формула 3 справедлива для любого промежутка, не содержащего точку х = 0; формула 10 - для интервала (-1,1) и т. п.
Замечание. В таблице основных интегралов вместо дг везде можно записать к = к(дс), где «(дс) - любая дифференцируемая функция независимой
Переменной дс: ^е^и=и+С,
При использовании формул этой таблицы для преобразования подынтегрального выражения к виду /(х)с1х = %(и)с1и применяются простейшие преобразования дифференциалов: 1) с1х = с1(х + Ь), где Ь = сопз1, 2) йх = = — ({(ах), а*О,
А
3) с1х = (1/а)с1(ах+Ь), аф 0, 4) хЛх = (1/2)с1 (дс2 + Ь), 5) зтдсаЬс = <!(-создс), 6) созда&с = 4 (зтдс), 7) ф' (дс) Ах = с!<р (дс).
Например,
^ зт 5хс1х = ^ зт 5дс у й (5дс) = ^ 51П Ъхй (5дс) = - + С, ¦
Г^= [1^1^,I «НС.
.1 дс +1 ^ дс +1 2 ^ дс +1 2 -
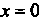
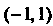
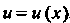
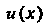
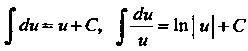
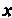
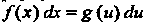
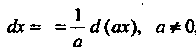
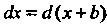
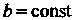
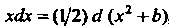
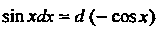
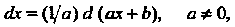
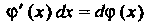

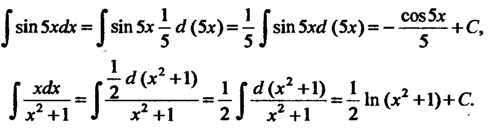
К наиболее важным методам интегрирования относятся следующие:
1) непосредственное интегрирование; 2) метод замены переменной; 3) метод интегрирования по частям.
| < Предыдущая | Следующая > |
|---|