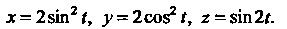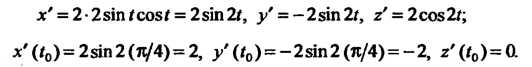15.13. Уравнения касательной к пространственной линии. Кривизна пространственной линии
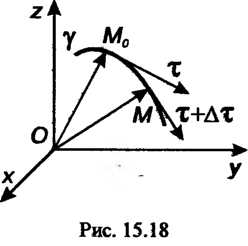
Рассмотрим пространственную линию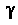 (рис. 15.18), заданную векторнопараметрическим уравнением
(рис. 15.18), заданную векторнопараметрическим уравнением
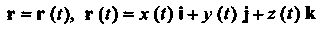
(15.23)
Или параметрическими уравнениями
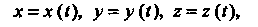
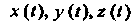
Где х (/), у (;), 2 (I) — дифференцируемые функции переменной (. Зафиксируем значение 10 параметра I, ему соответствует точка Л/0(х0, у0,20), где х0 = х (/0), Уо=У(*о)> 20=2(/0).
Уравнения касательной к пространственной линии (15.24) в точке М0(х0,у0,20) имеют вид
*~*о _У~Уо 2~2о П5 25ч *'(*„) у'Но) 2'(‘оУ '
Нормальной плоскостью к пространственной линии в данной ее точке М называется плоскость, проходящая через точку М и перпендикулярная касательной к данной кривой в той же точке.
Нормальная плоскость к линии (15.24) в точке М0(х0,у0,г0) имеет уравнение
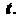
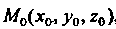
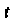
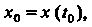
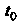
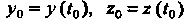
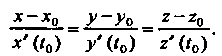
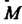
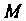
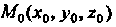
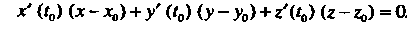
*' (*о) (х-х0) + / (10) (у - у0) + г'((0) (г-го) = О. (15.26)
Если 5 — длина дуги, то единичный вектор касательной X к линии у определяется формулой (15.22). Придав аргументу I приращение Д/, получим точку М линии у и соответствующий вектор касательной г + Дг. Степень изогнутости кривой можно характеризовать скоростью поворота вектора г.
Кривизной к линии у в точке М0 называется модуль производной вектор-функции т = г (а) в данной точке, т. е.
<&
С1з
Это определение равносильно определению кривизны плоской кривой. Кривизна линии, заданной уравнениями (15.24), выражается формулой
,_|[Г",Г']|
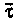
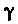
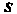
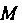
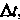
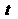
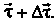
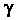
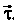
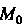
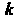
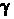
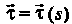
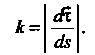
(15.27)
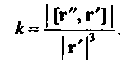
(15.28)
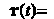
Кривизну линии можно выразить в координатах. Поскольку т(г)= ={40, у(0, г«)Ь г'(1) = {д:'(<), у'Ц), г’(()}, г"(0 = {х"(0, у"«),г"(0}, то
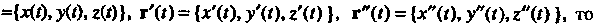
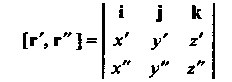
(15.29)
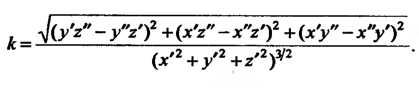
(1530)
Отметим, что формула (15.11) является частным случаем формулы (15.30). Пример 15.17. Записать уравнения касательной, уравнение нормальной плоскости и вычислить кривизну линии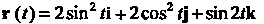 В точке,
В точке,
Для которой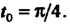
Перейдем к параметрическим уравнениям данной линии
Найдем координаты точки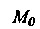
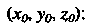
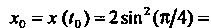
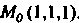
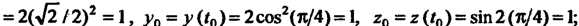
Найдем производные функций (I) и их значения при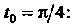
В соответствии с равенствами (15.25) получаем уравнения касательной к данной линии
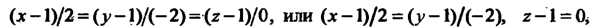
Подставляя соответствующие значения в формулу (15.26), находим уравнение нормальной плоскости: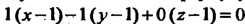 , или
, или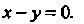
Для вычисления кривизны линии в точке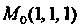 Нужны значения
Нужны значения
Вторых производных функций (I) при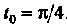 . Так как.
. Так как.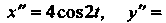
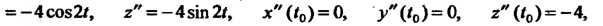 То по
То по
Формуле (15.30) находим 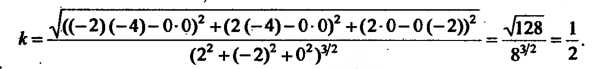
Глава 16
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
| < Предыдущая | Следующая > |
|---|