15.12. Дифференцирование вектор-функций

Предел отношения приращения вектор-функции к приращению аргумента, когда последнее стремится к нулю, называется производной вектор-функции и = и (у) в точке V:

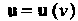
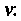
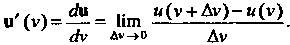
„» = ^ = Нт

Ду

Необходимым и достаточным условием существования производной вектор-функции

И(у) = {-*(у), у (у), г(у)}  (15.20)

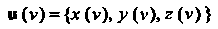
В некоторой точке является дифференцируемость функций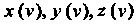В

Этой точке; причем в данном случае

?

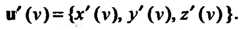Правила дифференцирования вектор-функции аналогичны правилам обычного дифференциального исчисления. Если-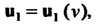

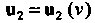Дифференцируемые вектор-функции скалярного аргумента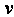, •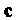- постоянный вектор,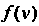- дифференцируемая скалярная функция,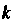- постоянная скалярная величина,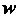- скалярный аргумент, связанный с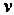Формулой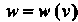, где

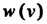- дифференцируемая функция, то эти правила дифференцирования выражаются следующими формулами:

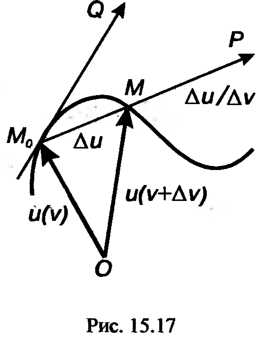
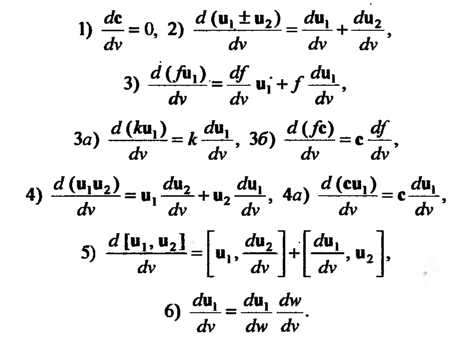
Геометрический смысл производной Производная вектор-функции в данной точке есть вектор, направленный по касательной к годографу данной вектор-функции в соответствующей точке (рис. 15.17).

Отметим, что при другом значащи v получим новое значение, т. е. производная вектор-функции также является вектор-функцией. Вектор-функция, имеющая производную, называется дифференцируемой.

Дифференциалом вектор-функции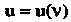 называется произведение её производной на дифференциал аргумента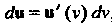, где

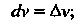Отсюда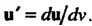

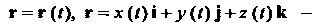
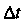
Векторное уравнение движения точки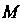В пространстве. Приращению времени 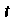Соответствует приращение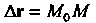Вектор-функции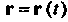. Отношение

Пусть

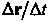Называется вектором средней скорости, этот вектор направлен по прямой 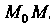. Предел указанного отношения при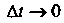Называется вектором скорости

В момент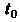(или вектором мгновенной скорости), обозначим его через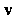, т. е.

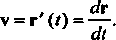
(15.21)

Следовательно, вектор мгновенной скорости (или вектор скорости) движущейся точки направлен по касательной к ее траектории. Вектор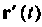Характеризует направление и быстроту движения точки.

Если для вектор-функции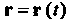В качестве параметра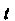Выбрать длину дуги

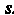, отсчитываемой от некоторой точки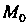, то производная вектор-функции будет равна единичному вектору, направленному по касательной. Обозначив этот вектор через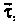, получим

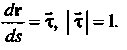
(15.22)

Второй производной вектор-функции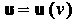Называется производная от ее

Производной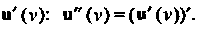

Для функции (15.20) имеем

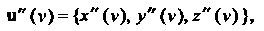
Если существуют вторые производные функций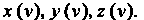

Аналогично определяются производные более высокого порядка для вектор-функции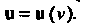

< Предыдущая		Следующая >