15.11. Переменная векторная величина. Вектор-функция скалярного аргумента

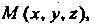
Рассмотрим точку М (х, у, г), движущуюся по некоторой линии у в пространстве (рис. 15.15). Радиус-вектор г = ОМ точки М будет иметь определенное направление и длину в фиксированный момент времени I. С течением времени направление и длина вектора ОМ будут изменяться.

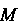
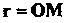
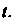
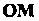
Таким образом, здесь имеем дело с переменным вектором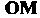Или с переменной векторной величиной

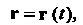(15.16)

Зависящей от времени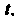Равенство (15.16) называется векторным уравнением движения точки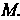

Координаты  переменного  вектора

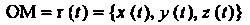Являются также переменными величинами (скалярными), зависящими от времени f: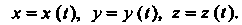

Уравнения (15.17) являются параметрическими уравнениями рассматриваемой линии

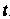Переменная векторная величинаНазывается вектор-функцией (или векторной функцией) скалярного аргумента, если каждому значению 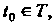Где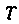— некоторое множество действительных чисел, соответствует определенный вектор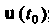; в этом случае пишут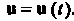

Бели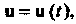То и проекции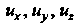Переменного вектора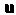На оси декар

Товой системы координат будут (скалярными) функциями аргумента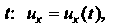

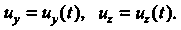
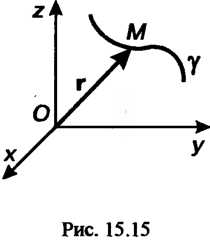
(15.17)

Пример вектор-функциискалярного аргумента Дает рассмотренный выше случай радиус-вектора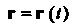Точки, движущейся по некоторой линии в

Пространстве.

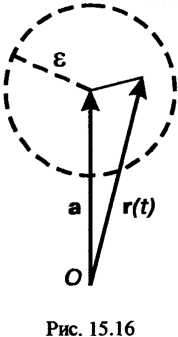
Годографом переменной векторной величины называется геометрическое место концов векторов всех ее отдельных значений при условии, что они отложены из одной точки. Годографом постоянного вектора являетсяточка (конец вектора). Годограф вектор-функции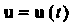Представляет собой некоторую ли

Нию. Если вектор сохраняет постоянную длину, то его годограф - линия, лежащая на сфере. Г одографом ра-диуса-вектора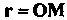Движущейся точки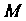Является

Траектория этой точки.

Пусть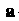- некоторый вектор (постоянный) и 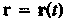некто p-функция, определенная в некоторой окрестности точки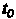, кроме, быть может, самой точки.

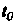Вектор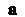Называется пределом вектор-функции

При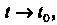Если для любого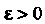Существует

Такое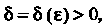Что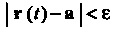Для всех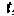, удовле

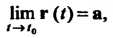
Итг(0 = а,  (15.18)

<-»<0

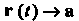
Г (О -» а при I -»10.

Очевидно, равенство (15.18) эквивалентно равенству

Нт I г (0—а 1 = 0.  (15.19)

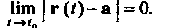
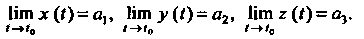
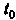
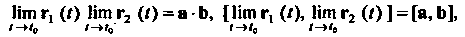
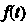
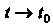
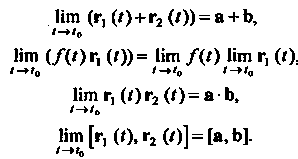
Вектор-функция г = г (0, определенная в точке 10 и некоторой ее окрестности, называется непрерывной в этой точке, если Нт г (0 = г (10).

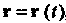
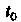
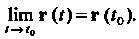
Если г (1) = {х(1),у(1),2(1)} и а = (аиа2,а3), то равшство (15.18) выполняется тогда и только тогда, когда  \ Нт х (!) = о,, Нт у (I) = а2, Нт г (I) = о3.

Если вектор-функции г, (<) и г2 (I) определены в некоторой окрестности точки 10 и существуют пределы

Нт г, (0 = а, Нт г, (I) = Ь,

<-»<0 <-»<0

Нт г, (() Нт г2 (() = а - Ь, [ Нт г, (/), Нт г2 (/) ] = [а, Ь], скалярная функция ДО имеет предел при ( —»(0, то существуют также пределы

Нт (г, (<)+г2 (/))= а + Ь,

Нт (/(Ог, (0)= Нт /(0 Нт г, (0,

Нт г, (0г2 (0=а Ь,

Нт[г, (0,г2 (0] = [а, Ь].

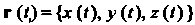
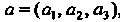
Из эквивалентности условий (15.18) и (15.19) следует, что вектор-функция г (0 = (0. У (0.2 (0 } непрерывна в точке г0 тогда и только тогда, когда непрерывны в ней функции х (0, У (0.2 (0-

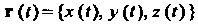
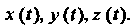
< Предыдущая		Следующая >