15.10. Окружность кривизны. Центр и радиус кривизны. Эволюта и эвольвента
Радиусом кривизны данной линии в данной ее точке называется величина К, обратная кривизне к этой линии в рассматриваемой точке:
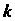
(15.13) К \Уа\
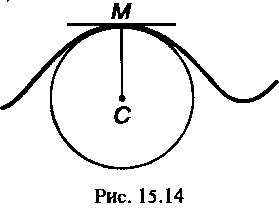
На нормали к кривой в точке М отложим отрезок МС = К в сторону вогнутости кривой (рис. 15.14). Точка С называется центром кривизны данной линии в точке М. Окружность радиуса К с центром в точке С называется окружностью кривизны этой линии в точке М. Очевидно, в данной точке М кривизна кривой и кривизна окружности равны между собой.
Координаты центра кривизны определяются формулами
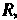
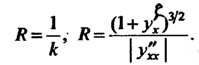


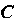
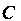
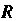
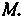
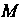
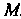
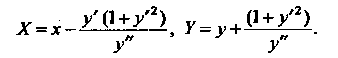
У" У
Если кривая задана параметрическими уравнениями х=х(1), У = У(0. то формулы (15.14) с учетом равенств (14.20) и (14.22) примут вид
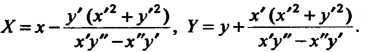
+ (15.15)
Щ Множество всех центров кривизны дан
Ной линии называется ее эволютой. По отношению к своей эволюте исходная линия называется эвольвентой (или разверткой).
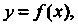
Если линия задана уравнением у = /(х), то уравнения (15.14) можно рассматривать как параметрические уравнения ее эволюты (с параметром х).
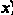
В случае параметрического задания кривой уравнения (15.15) являются параметрическими уравнениями эволюты (входящие в правые части этих уравнений величины зависят от параметра I).
| < Предыдущая | Следующая > |
|---|