15.09. Кривизна плоской кривой
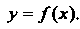
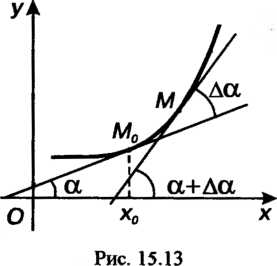
Рассмотрим плоскую линию, определяемую уравнением у = /(х). Проведем касательную к этой линии в ее точке М0(х0, у0); обозначим через а угол, образо-
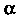
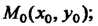
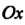
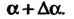
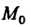
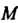
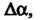
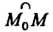
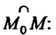
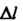
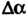
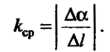
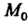
Кривизной линии в данной точке М0 называется предел средней кривизны дуги
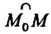
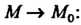
М0М при М -» М0\
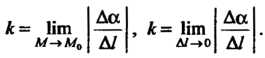
А /м
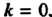
(15.9)
Отметим, что для прямой к = 0, а для окружности радиуса К кривизна к = = 1/К.
Кривизна линии, заданной уравнением у= Дх), в точке Л/0(*о, у0) вычисляется по формулам
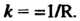
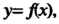
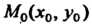
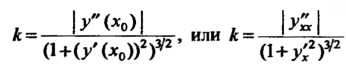
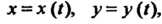
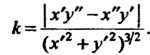
(15.11)
(15.12)
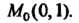
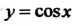
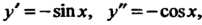
Ванный касательной с осью Ох (рис. 15.13). Пусть касательная в точке М образует с осью Ох угол а + Да.
Угол Да между касательными в указанных точках называют углом смежности. Можно сказать, что при переходе из точки М0 в точку М данной линии касательная к ней повернулась на угол Да, которому будем приписывать соответствующий знак в зависимости от направления поворота.
П
Средней кривизной дуги М0М данной линии называется абсолютное значе-
П
Нйе отношения угла смежности Да к длине А1 дуги М0М:
Да
ОяуыгР - ~~ (1510>
Если линия задана параметрическими уравнениями х = х (I), у = у ((), то с учетом (14.2р) и (14.22) формула (15.10) принимает вид
_ \х'у"-х"у'\
{х’2+у'2)^'
Кривизна линии, заданной уравнением р = р (ф) в полярных координатах, вычисляется по формуле
I о - - О „I
-рр
(Р'2+Р2)*2
Пример 15.16. Найти кривизну косинусоиды у = соз* в точке М0(0,1). Поскольку у' = -8ШХ, у" = - соях, кривизна косинусоиды в ее произвольной точке определяется формулой
|-со8х|
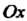
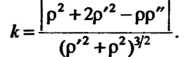
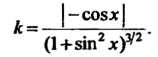
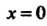
При х = 0 получаем к = 1/(1+0)у2 = 1.
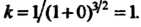
| < Предыдущая | Следующая > |
|---|