15.08. Дифференциал длины дуги кривой

 

Пусть на отрезке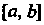Задана дифференцируемая функция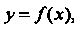, графи

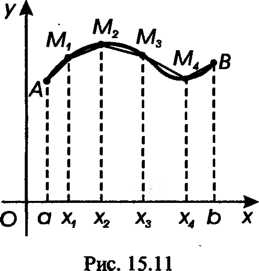
Ком которой является дуга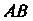(рис. 15.11). Отрезок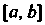Разобьем на и частей точками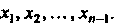Этим точкам будут соответствовать точки,

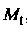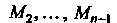Дуги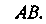Соединим их отрезками прямых. Ломаную

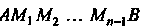Называют вписанной в дугу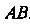. Периметр этой ломаной обозначим через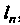, т. е.

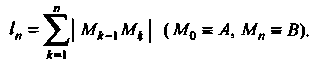
Длиной дуги называется предел периметра вписанной в нее ломаной, когда число звеньев Мк.)Мк неограниченно возрастает, а длина наибольшего из них стремится к нулю:

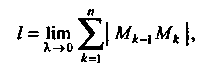
Где X - длина наибольшего звена

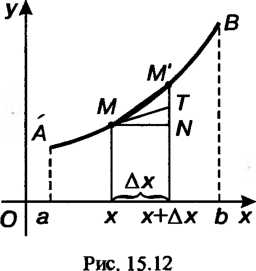
Будем отсчитывать длину дуги от некоторой ее точки, например, от точки А; пусть в точке М (х, у) длина дуги АМ равна /, а в точке М\х + Дх, у + Ау)

Длина дуги АМ' равна /+Д/, где А1 - длина дуги ММ' (рис. 15.12). Очевидно, 1 = 1 (х), бесконечно малая дуга линии и стягивающая ее хорда эквивалентны:

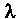
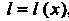
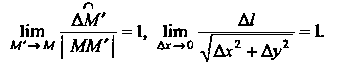
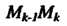
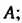
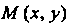
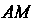
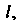
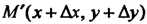
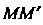
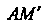
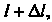
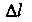
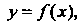
Дифференциал длины дуги плоской кривой, заданной уравнением у = /(х), выражается формулой

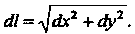
<11 = л]с1х2 +ф2.

Эта формула имеет простой геометрический смысл: она выражает теорему Пифагора

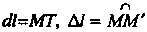
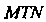
Для бесконечно, малого треугольника МШ (рис. 15.12, <й=МТ, Д/ = ММ'). Дифференциал дуги пространственной кривой выражается формулой

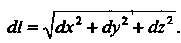
<11 = -^сЬ2 + дуг; + дг2.

< Предыдущая		Следующая >