15.03. Экстремум функции
Рассмотрим функцию у = Дх), областью определения которой является промежуток (а, Ъ).
Если можно указать такую 6-окрестность точки принадлежащую промежутку (а, Ь\ что для всех хеО(х,,8), хФх,, выполняется неравенство
Дх,)>/(х), (15.4)
То У\~/\(х\) называют максимумом функции у = Дх) (рис. 15.2).
Максимум функции у-Дх) обозначим через шах Дх).
Если можно указать такую 8-окрестность точки хг, принадлежащую промежутку (а, Ь), что для всех х е О (хг, 8), неравенство
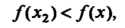
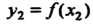
То У г = Дх2) называют минимумом функции у = Дх) (см. рис. 15.2).
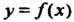
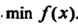
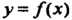
Минимум функции у = Дх) обозначим через шт Дх).
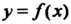
Другими словами, максимумом (минимумом) функции у = Дх) называют такое ее значение, которое больше (меньше) всех других значений, принимаемых в точках, достаточно близких к данной и отличных от нее.
Замечание 1. Максимум функции, определяемый неравенством
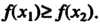
(15.4), называется строгим максимумом; нестрогий максимум определяется неравенством /(х,)^ Дхг).
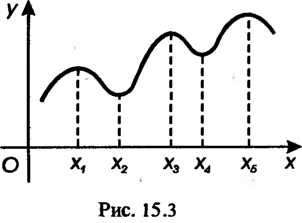
Замечание 2. Максимум и минимум функции имеют локальный характер (это наибольшее и наименьшее значения функции в достаточно малой окрестности соответствующей точки); отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 15.3). Вследствие этого максимум (минимум) функции называют локальным максимумом (локальным минимумом) в отличие от абсолютного максимума (минимума) - наибольшего (наименьшего) значения в области определения функции.
Максимум и минимум функции называются экстремумом. Латинское extremum означает «крайнее» значение. Значение аргумента, при котором достигается экстремум, называется точкой экстремума Необходимое условие экстремума выражается следующей теоремой.
Теорема 15.3. В точке экстремума дифференцируемой функции производная ее равна нулю.
Теорема имеет простой геометрический смысл: касательная к графику дифференцируемой функции в соответствующей точке параллельна оси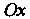 (см. рис. 15.2).
(см. рис. 15.2).
Замечание 3. Если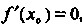 , то отсюда еще не следует, что
, то отсюда еще не следует, что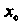
Точка экстремума. Например, для функции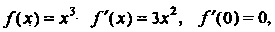 Но
Но
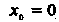 Не является точкой экстремума, так как
Не является точкой экстремума, так как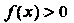 При
При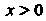 И
И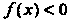 При
При
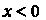 (неравенство (15.4) или (15.5) здесь не выполняется).
(неравенство (15.4) или (15.5) здесь не выполняется).
Замечание 4. Функция может достигать экстремума также в точке, в которой производная не существует. Например, функция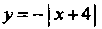 Не имеет
Не имеет
Производной в точке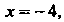 Но достигает в ней максимума:
Но достигает в ней максимума: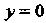 При
При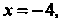 А
А
Для всякой другой точки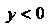 (рис. 15.4, а). Функция
(рис. 15.4, а). Функция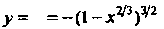 Не
Не
Имеет конечной производной в точке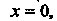 Поскольку
Поскольку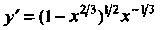 При
При
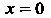 Обращается в бесконечность, но в этой точке функция имеет минимум:
Обращается в бесконечность, но в этой точке функция имеет минимум: 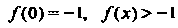 При
При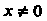 (рис. 15.4, б).
(рис. 15.4, б).
Говорят, что функция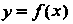 Меняет знак при переходе через точку
Меняет знак при переходе через точку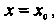 , если
, если
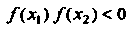 Для любых
Для любых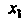 И
И Из некоторой окрестности этой точки, удовлетво-
Из некоторой окрестности этой точки, удовлетво-
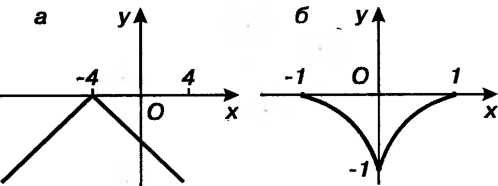
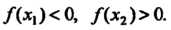
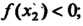
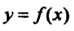
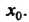
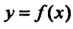
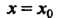
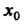
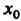
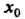
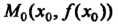
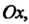
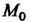
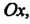
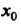
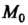
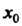
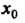
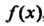
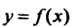
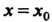
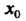
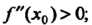
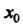
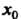
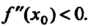
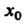
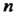
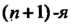
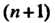
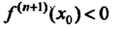
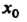
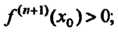
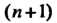
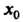
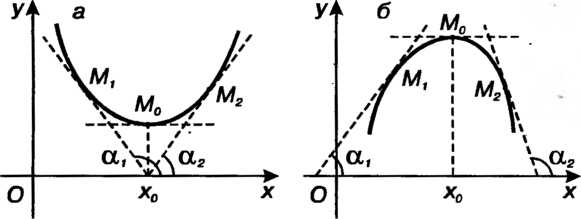
Ряющих неравенствам х, < х0 < х2; знак меняется с плюса на минус, если /(*,)>(), а /(х2)< 0; знак меняется с минуса на плюс, если /(л,)<0, /(х2)>0.
Формулируя теоремы 15.4 и 15.5, будем предполагать, что функция у = /(*) дифференцируема в некоторой окрестности точки х0.
Теорема 15.4. Если при х = х0 производная функции у — /(х) равна нулю и меняет знак при переходе через это значение, то х0 является точкой экстремума, причем: I) х0 - точка максимума, если знак меняется с плюса на минус; 2) х0 - точка минимума, если знак меняется с минуса на плюс.
Теорема имеет следующий геометрический смысл: если в точке М0(х0, /(х0)) графика дифференцируемой функции касательная параллельна оси Ох, в точках слева от М0 образует тупой угол с осью Ох, в точках справа - острый, то х0 - точка минимума (рис. 15.5, о); если в точках слева от М0 касательная образует с осью Ох острый угол, а в точках справа - тупой, то х0 - точка максимума (рис. 15.5,6).
Замечание. Теорема верна и в случае, если х0 - точка непрерывности функции /(х), производная в ней не существует и меняет знак при переходе через эту точку.
Достаточное условие экстремума можно выразить также с помощью второй производной.
Теорема 15.5. Если в точке х = х0 первая производная функции у = /(х) равна нулю, а вторая производная отлична от нуля, то х0 является точкой экстремума, причем: 1) х0 - точка минимума, если /"(хь) > 0; 2) х0 - точка максимума, если /"(ло)<0.
Теорема 15.6. Пусть в точке х0 первые п производные равны нулю, а (и +1) - я отлична от нуля и непрерывна в этой точке, тогда: 1) если (и + 1) — четное число, то х0 — точка экстремума: точка максимума при /^п+|)(х0) < 0 и точка минимума при /("+|)(л0)>0; 2) если (и + 1) - нечетное число, то х0не является точкой экстремума.
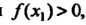
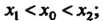
Пример 15.7. Найти экстремумы функции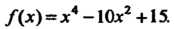
Поскольку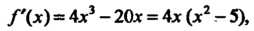 То точками, для которых
То точками, для которых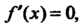
Являются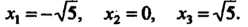 Исследуем знак второй производной
Исследуем знак второй производной
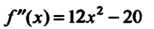 В этих точках:
В этих точках: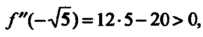
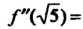
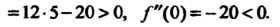
Следовательно,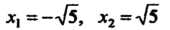 - точки минимума,
- точки минимума,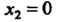 - точка мак
- точка мак
Симума;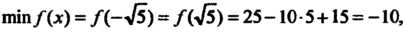
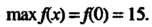
Пример 15.8. Вычислить значения экстремумов функции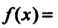
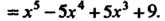
Первая производная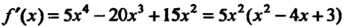 Обращается в
Обращается в
Нуль при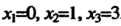 . Вторая производная
. Вторая производная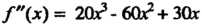 В этих точках принимает соответственно значения
В этих точках принимает соответственно значения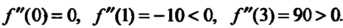
Следовательно,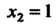 - точка максимума,
- точка максимума,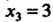 - точка минимума, причем
- точка минимума, причем
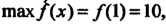
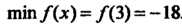 . Чтобы исследовать точку
. Чтобы исследовать точку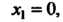
Обратимсяк третьей производной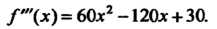 Поскольку
Поскольку
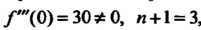 , то
, то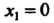 Не является точкой экстремума.
Не является точкой экстремума.
Пример 15.9. Найти точки экстремума функции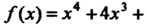
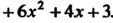
Первая производная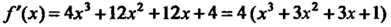 Равна ну
Равна ну
Лю в единственной точке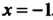 . Находим выражения последующих производных
. Находим выражения последующих производных
И их значения в критической точке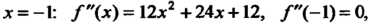
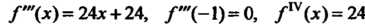 . Поскольку
. Поскольку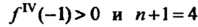
(четное число), тс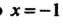 — точка минимума, причем
— точка минимума, причем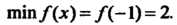
| < Предыдущая | Следующая > |
|---|