15.04. Направления выпуклости, точки перегиба
График функции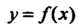 Называется выпуклым вниз (вогнутым вверх) в дан
Называется выпуклым вниз (вогнутым вверх) в дан
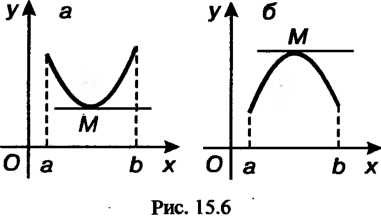
Ном промежутке, если он целиком расположен выше касательной в его произвольной точке (рис. 15.6, а).
График функции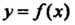 Называется выпуклым вверх (вогнутым вниз) в дан
Называется выпуклым вверх (вогнутым вниз) в дан
Ном промежутке, если он целиком расположен ниже касательной в его произвольной точке (рис. 15.6, б).
Теорема 15.7. Если вторая производная функции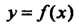 В данном
В данном
Промежутке положительна, то график ее является выпуклым вниз в этом промежутке; если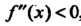 , то график функции является
, то график функции является
Выпуклым вверх в соответствующем промежутке.
Точкой перегиба графика функции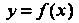 Называется такая его точка
Называется такая его точка
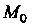 (рис. 15.7), в которой выпуклость меняется на вогнутость (по отношению к одному и тому же направлению: вверх или вниз).
(рис. 15.7), в которой выпуклость меняется на вогнутость (по отношению к одному и тому же направлению: вверх или вниз).
Теорема 15.8. Если вторая производная функции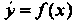 При
При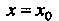 Об
Об
Ращается в нуль и меняет знак при переходе через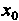 , то
, то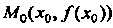 —
—
Точка перегиба графика этой функции.
Пример 15.10. Найти интервалы выпуклости и точки перегиба графика функции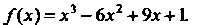
Поскольку вторая производная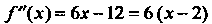 Обращается в нуль при
Обращается в нуль при
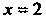 И меняет знак при переходе через это значение, то
И меняет знак при переходе через это значение, то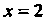 - абсцисса точки перегиба, ордината этой точки
- абсцисса точки перегиба, ордината этой точки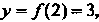 Т. е.
Т. е.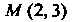 — точка перегиба.
— точка перегиба.
Так как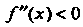 При
При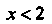 И
И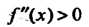 При
При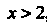 , то график функции является
, то график функции является
Выпуклым вверх в интервале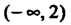 И выпуклым вниз в интервале
И выпуклым вниз в интервале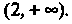
| < Предыдущая | Следующая > |
|---|