15.02. Признаки постянства. Убывание и возрастанияие функции
Необходимое и достаточное условие постоянства функции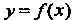
Выража
Ется равенством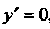
, т. е.
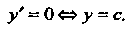
(15.3)
Функция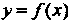
I называется возрастающей в промежутке
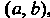, если для
Любых двух значений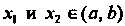
Из неравенства
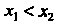Следует неравенство
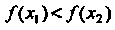
(рис. 15.1, а).
Функция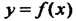
Называется убывающей в некотором промежутке, если для
Любых двух значений, принадлежащих этому промежутку, из неравенства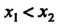
следует неравенство
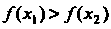(рис. 15.1,6).
Достаточное условие возрастания (убывания) функции выражается следующей теоремой.
Теорема 15.2. Если в данном промежутке производная функции положительна, то функция возрастает в этом промежутке; если производная отрицательна, то функция убывает в соответствующем промежутке.
->
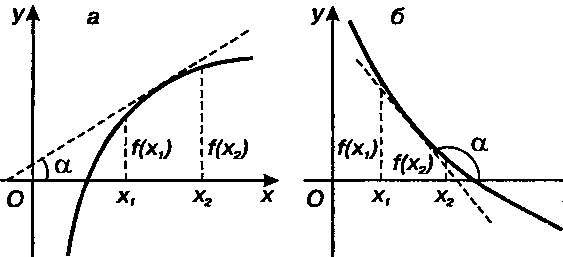
X
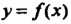
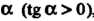
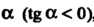
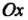
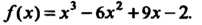
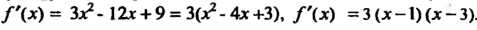
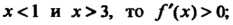
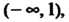
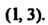
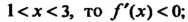
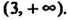
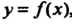
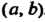
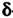
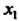
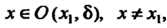
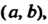
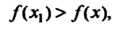
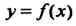
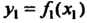
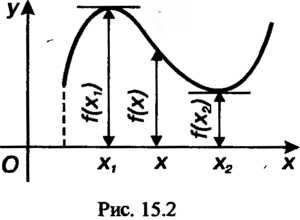
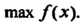
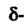
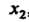
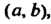
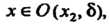
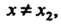
(15.5)
Замечание. Теорема имеет простой геометрический смысл. Если в некотором промежутке касательная к графику функции у-/(х) образует с осью Ох острый угол а (18 а > 0), то функция возрастает в этом промежутке (рис. 15.1, а). Если касательная к графику образует с осью Ох тупой угол а (1§ сх < 0), то функция убывает (рис. 15.1, б).
Пример 15.6. Найти промежутки возрастания и убывания функции Дх) = х3-6хг+9х-2.
Находим производную функции и разлагаем на множители соответствующий квадратный трехчлен: /'(¦*) = 3.x2 - 12х + 9 = 3(д^ - Ах +3), /'(х) = 3 (х -1) (х - 3).
Если х < 1 и х > 3, то /'(х) > 0; функция возрастает в интервалах (- 1), (3, + о®). Если 1 < х < 3, то /'(х) < 0; функция убывает в интервале (1,3).
| < Предыдущая | Следующая > |
|---|
