15.01. Правило Лопиталя - Бернулли
При исследовании функций может появиться необходимость нахождения предела дроби /(х)/(р(х), числитель и знаменатель которой при х —> а стремятся к нулю или к бесконечности. Нахождение таких пределов называют раскрытием неопределенностей соответствующего виаа. Основой его является правило Лопиталя - Бернулли, выражаемое следующей теоремой.
Теорема 15.1. Если функции /(х) и <р (х) дифференцируемы в окрестности точки х = а, обращаются в нуль в этой точке и существует предел отношения /’(х)/<р' (х) при х —»а, тогда существует предел отношения самих функций, равный пределу отношения производных
Нш = 1ип /М. (15.1)
Х->а <р (дс) х->а ф' (х)
Замечание 1. Теорема верна и в том случае, когда функции /(х) и Ф (х) не определены в точке х = а, но Нт /(*)*= 0, Иш ф (х) = 0.
Х—>а х—>о
Замечание 2. Теорема верна и в случае а = т. е. когда 1нп /(*) = 0, Нш ф (х) = 0.
Х~»оо X —> оо
Замечание 3. Если /'(а) = 0, ф'(о) = 0, функции /'(х), ф'(я) дифференцируемы в окрестности точки х = а и существует предел отношения /"(¦*)/ф"(*) при х —» а, то
Нш = Нш (15.2)
Х-ю ф' (х) х->а ф" (*)
Другими словами, правило Лопиталя - Бернулли при вьшолнении соответствующих условий можно применять несколько раз.
Правило Лопиталя - Бернулли применимо и при раскрытии неопределенно-
„ •» 0 стей вида —, поскольку ее можно привести к неопределенности вида —, пред-
Оо 0
Ставив рассматриваемую дробь так:
/(*)_ 1.1 фМ фМ /М
С помощью тождественных преобразований к основному виду — или — можно све-
0 М
Сти неопределенности других видов, таких, как 0 ¦ <=“, со-со, 1”, о0, со0.
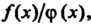
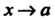
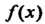
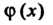
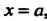
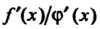
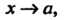
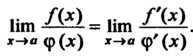
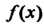
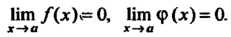
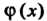
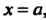
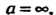
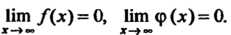
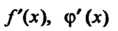
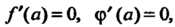
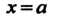
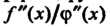
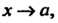
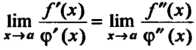
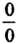
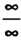
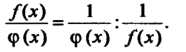
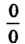
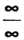
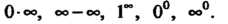
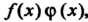
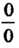
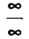
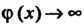
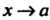
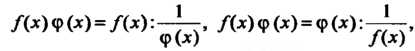
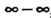
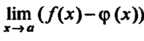
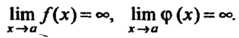
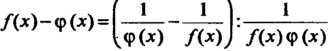
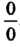
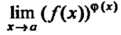
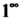
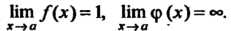
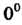
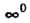
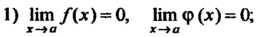
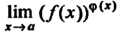
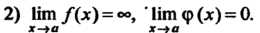
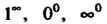
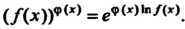
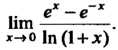
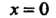
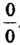
Неопределенность вида О-оо, т. е. произведение /(х)ф (х), где /(х)-»0, Ф (х) —» оо при х -» а, приводится к виду — или — по формулам
О ОО
/(*) Ф (*) = /(*):-7-т, /(¦*) ф (*) = ф (х):¦-1—, ф(*) /(¦*) а затем применяется правило Лопитапя - Бернулли.
Аналогично раскрывается неопределенность вида оо-оо, т. е. находится предел Нт (/(х)-ф(х)) при условии, что Нт/(х) = оо, Нт ф (х) = С помощью
Х->о х-»о х~>а
Преобразования /(х)-ф(х) = [—----?—I:-5- эта неопределенность
^ф(х) Дх)) /(х)ф(х)
О ,
Сводится к неопределенности вида —.
Раскрыть неопределенность вица 1~ — значит найти предел Иш (/(-х))ф(х)
Х-*а
При условии, что Нт Дх) = 1, Нт ф (х) =
Х~>а х -*а
Раскрыть неопределенности вида 0°, оо° - значит найти предел Нт (/(х))ф(г) при соответствующем условии: 1) Нт/(х) = 0, Нтф(х) = 0;
Х-*а х-»о х —> а
2) Нт Дх) = »°, Нтф(х) = 0.
Х-*а х->й
Неопределенности 1”, 0°, °о° раскрываются способом, в котором используется тождество (Дх)Г<*> = е9М'п/(г).
При раскрытии этих неопределенностей данное выражение предварительно логарифмируют и находят предел его логарифма.
Правило, выражаемое теоремой 15.1, сформулировано швейцарским математиком И. Бернулли (1667 - 1748) и’ опубликовано в 1696 г. в первом печатном учебнике анализа бесконечно малых, написанном французским математиком Г. Лопиталем (1661 - 1704).
ДХ _ —X
Пример 15.1. Найти Нт-.
*-»<> 1п (1 + х)
При х = 0 числитель и знаменатель дроби обращаются в нуль, имеем неопределенность вида Чтобы раскрыть ее, применяем правило
Лопиталя — Бернулли:
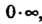
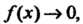
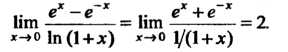
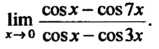
Для раскрытия этой неопределенности вида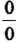 Правило Лопиталя - Бернулли необходимо применить дважды:
Правило Лопиталя - Бернулли необходимо применить дважды:
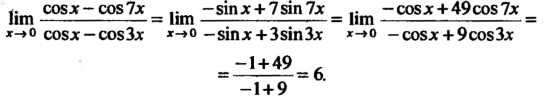
Пример 15.3. Найти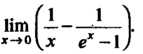 Здесь имеем неопределенность вида
Здесь имеем неопределенность вида Преобразуем данную разность
Преобразуем данную разность
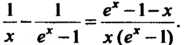
При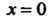 В правой части этого равенства имеем неопределенность вида
В правой части этого равенства имеем неопределенность вида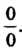
Применяя дважды правило Лопиталя — Бернулли, находим:
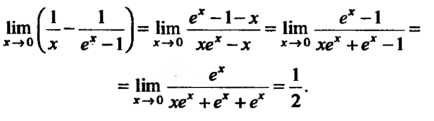
Пример 15.4. Найти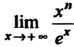 , где
, где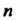 - натуральное число.
- натуральное число.
Применяя правило Лопиталя — Бернулли п раз, получаем
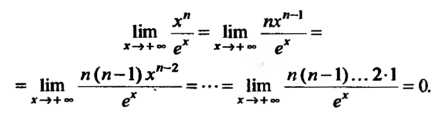
Следовательно, при неограниченном возрастании аргумента степенная функция растет медленнее показательной функции.
Пример 15.5.Найти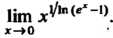
При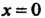 Получаем неопределенность вида
Получаем неопределенность вида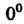 . Обозначим
. Обозначим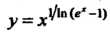 И
И
Прологарифмируем это равенство по основанию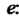
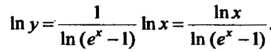
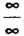
В правой части этого равенства при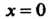 Имеем неопределенность вида
Имеем неопределенность вида
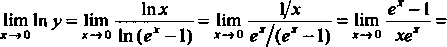
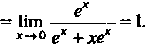
Следовательно,
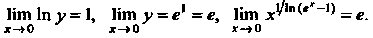
| < Предыдущая | Следующая > |
|---|