14.7. Формула Тейлора для некоторых функций
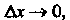
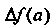
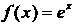
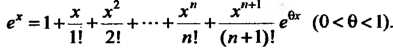
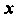
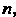
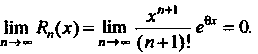
1! 2! и! (и+1)!
Отметим, что при любом х остаточный член формулы (14.41) стремится к нулю при неограниченном возрастании и, т. е.
И+1
(14.42)
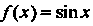
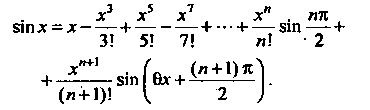
Остаточный член
\ х"+1 • (а, (и + 1)«
Формулы (14.42) также стремится к нулю при и —> <».
Формула (14.39) для функции /(-*) = со8я имеет вид
2! 4! 6! и! 2
Хп+1 (и + 1) я
+-со8 вх+^-
Каково бы ни было х, остаточный член формулы (14.43) стремится к нулю при и —» во.
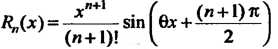
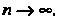
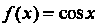
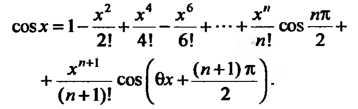
(14.43)
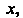
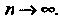
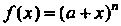
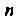
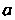
Для функции /(х) = (а+х)п, где а - действительное число, и - натуральное число, получаем
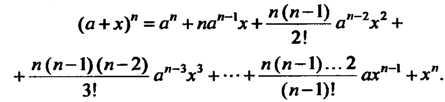
(а+х)" = а” + па"~1х + п(-п~1) а"~2х2 +
4 2!
+ ”(”-1)(”-2)а"-у + ...+ "("-!)¦ :2ах'-'+х". (14.44)
3! (и—1)!
Это равенство называется формулой бинома Ньютона.
Если в формуле (14.39) отбросить остаточный член, то получится приближенная формула
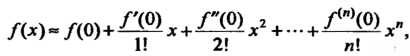(14.45)
Заменяющая данную функцию многочленом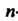
-й степени. Качество этой формулы оценивается двояко: указываются границы погрешности
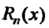С помощью выражения (14.38) для остаточного члена либо порядок малости этой погрешности при
'
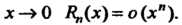В случае функции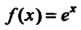
Получаем приближенную формулу
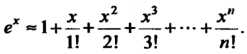(14.46)
Поскольку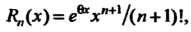
То например, при
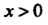Погрешность
Оценивается неравенствами
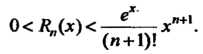(14.47)
В частности, при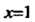
Получаем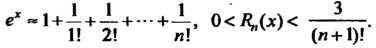
Если взять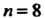
И произвести вычисления с пятью десятичными знаками, то получим
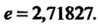Здесь верны первые четыре знака, так как ошибка
Не превосходит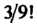
Или
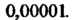
Взяв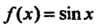
И положив в равенстве (14.42)
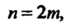Получим прибли
Женную формулу
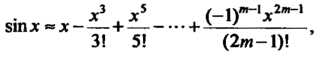(14.48)
Остаточный членчсоторой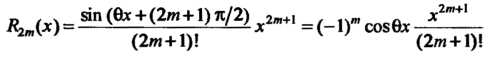 
оценивается соотношением
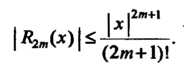
Погрешность приближенной формулы (14.49) выражается остаточным членом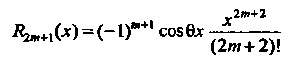 
и оценивается неравенством
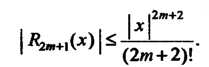
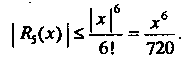
Пример 14.24. Вычислить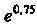
С точностью до
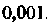Применяем формулу (14.46), полагая в ней
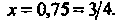Поскольку
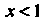И
Например, для формулы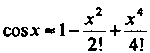
Погрешность
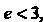То из формулы (14.47) следует, что
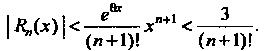
Требование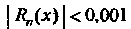
Будет выполнено, если
,
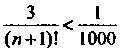Или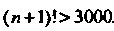
Это неравенство выполняется при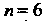
(тогда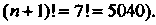
Значит, для вычисления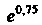
С заданной точностью в формуле (14.46) нужно
Взять шесть слагаемых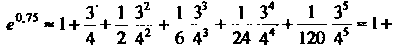
Глава 15
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
| < Предыдущая | Следующая > |
|---|
