14.6. Формула Тейлора
Формула
Называется формулой Тейлора с остаточным членом в форме Лагранжа:
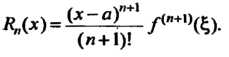(14.38)
Если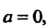
То формула принимает вид
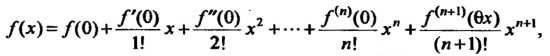
Где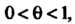
И называется формулой Маклорена.
Формулу (14.37) можно записать в виде
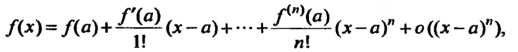
(14.40)
Где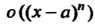
- бесконечно малая порядка выше
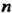-го по сравнению с
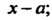Эта
Форма остаточного члена была указана Пеано.
Замечание. Если в формулах (14.37) и (14.40) перенести в левые части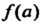 
И обозначить
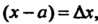Тогда
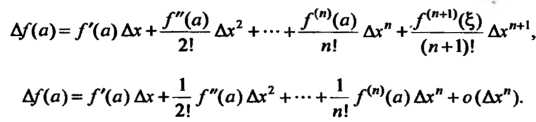
(14.39)
Если в этих формулах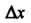
Заменить на
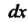И принять во внимание формулы (14.35), (14.36), то получим соответственно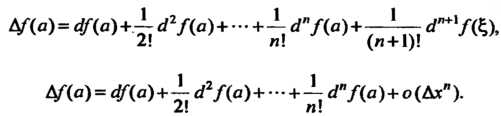 
Следовательно, если предположить, что Ах —> О, то по этим формулам из бесконечно малого приращения функции Д{(а) можно выделить не только его главный член — первый дифференциал, но и члены более высоких порядков малости, совпадающие (с точностью до факториалов в знаменателях) с последовательными дифференциалами с12/(а), с! ъ/(а),
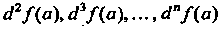
| < Предыдущая | Следующая > |
|---|
