14.4. Дифференциал функции
Понятие дифференциала. Применение дифференциала в приближенных вычислениях. Рассмотрим функцию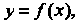 Определенную в некотором про
Определенную в некотором про
Межутке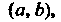 И ее приращение
И ее приращение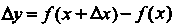 В точке
В точке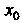 , где
, где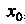
Если приращение функции представимо в виде
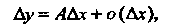 (14.23)
(14.23)
Где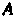 - постоянная,
- постоянная,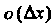 - бесконечно малая высшего порядка по сравнению с
- бесконечно малая высшего порядка по сравнению с
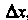 , то слагаемое
, то слагаемое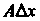 Называют дифференциалом функции
Называют дифференциалом функции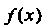 В точке
В точке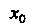 И
И
Обозначают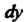 Или
Или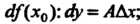 Функцию
Функцию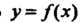 В этом случае называют
В этом случае называют
Дифференцируемой в точке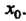
Если приращение функции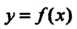 Представимо формулой (14.23), то
Представимо формулой (14.23), то
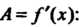 Следовательно,
Следовательно,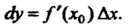 Так как
Так как
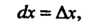 (14.24)
(14.24)
Т. е. дифференциал независимой переменной равен приращению этой переменной, то
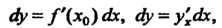 (14.25)
(14.25)
Откуда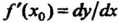 , т. е. производная равна отношению дифференциала функ
, т. е. производная равна отношению дифференциала функ
Ции к дифференциалу независимой переменной.
Формулу (14.23) можно записать так:
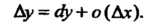 (14.26)
(14.26)
Дифференциал функции называют также главной линейной частью ее приращения.
Теорема 14.6. Бесконечно малое приращение функции эквивалентно ее дифференциалу при всех значениях независимой переменной, для которых производная функции конечна и отлична от нуля.
Из равенства (14.26) при достаточно малых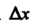 Получаем
Получаем
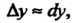 Или
Или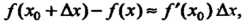 (14.27)
(14.27)
Откуда
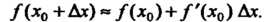 (14.28)
(14.28)
Формулы (14.27) и (14.28) применяются в приближенных вычислениях.
Пример 14.22. Вычислить значение дифференциала функции 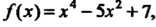 Когда аргумент
Когда аргумент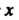 Меняется от
Меняется от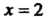 До
До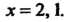 Найдем сначала выражение для дифференциала данной функции по формуле
Найдем сначала выражение для дифференциала данной функции по формуле
(14.25):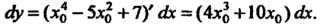 Так как
Так как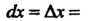
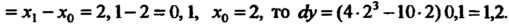
Пример 14.23. Вычислить приближенно значение функции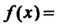
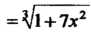 При
При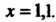
Значение аргумента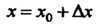 Представим в виде
Представим в виде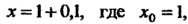
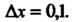 При
При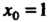 Легко вычисляются значения функции и ее производной
Легко вычисляются значения функции и ее производной
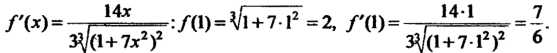
Эти значения входят в формулу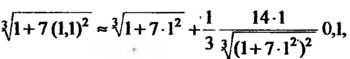 Полу
Полу
Ченную из формулы (14.28). Следовательно,
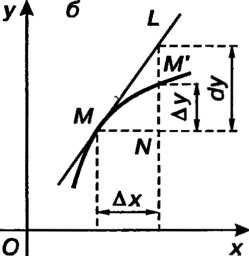
Геометрический смысл дифференциала. Дифференциал функции равен приращению ординаты касательной к графику функции в соответствующей точке, когда аргумент получает приращение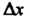 (рис. 14.4).
(рис. 14.4).
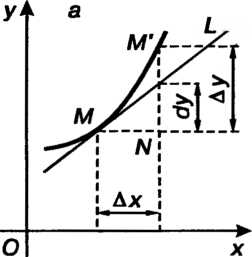
Отметим, что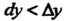 (рис. 14.4, а) или
(рис. 14.4, а) или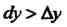 (рис. 14.4, б); если функция
(рис. 14.4, б); если функция
Равна постоянной, то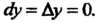
Физический смысл дифференциала. Рассмотрим прямолинейное движение точки по закону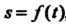 , где
, где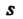 — длина пути,
— длина пути,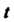 - время,
- время,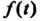 -дифференцируемая функция; тогда
-дифференцируемая функция; тогда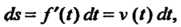 Где
Где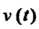 - скорость движения. Следовательно, дифференциал пути равен приращению пути, полученного в предположении, что, начиная с данного момента
- скорость движения. Следовательно, дифференциал пути равен приращению пути, полученного в предположении, что, начиная с данного момента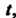 Точка движется равномерно, сохраняя приобретенную скорость.
Точка движется равномерно, сохраняя приобретенную скорость.
Свойства дифференциала. Дифференциал функции обладает свойствами, аналогичными свойствам производной.
1. Дифференциал постоянной равен нулю:
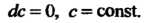 (14.29)
(14.29)
2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
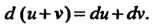 (14.30)
(14.30)
Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
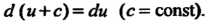 (14.31)
(14.31)
3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
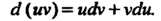 (14.32)
(14.32)
Следствие. Постоянный множитель можно выносить за знак дифференциала
4. Дифференциал частного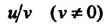 Двух дифференцируемых функций
Двух дифференцируемых функций
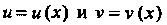 Определяется формулой
Определяется формулой
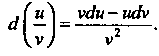 (14.34)
(14.34)
5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого-от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.
Основные дифференциалы:
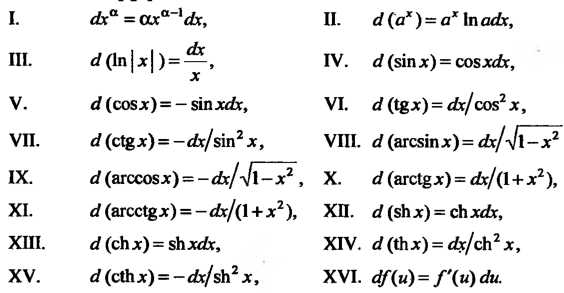
Дифференциалы высших порядков. Если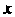 - независимая переменная и
- независимая переменная и 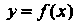 - дифференцируемая функция, то
- дифференцируемая функция, то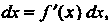 Т. е. дифференциал
Т. е. дифференциал
Функции есть функция, зависящая от двух аргументов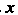 И
И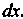 Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом). Считая
Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом). Считая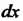 Постоянной, получаем, что
Постоянной, получаем, что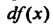 - функция одной переменной. Предположим, что функция
- функция одной переменной. Предположим, что функция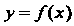 Имеет не только первую производную, но и
Имеет не только первую производную, но и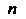 Последовательных производных
Последовательных производных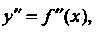
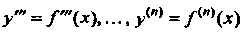
Дифференциал от дифференциала функции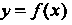 Называется вторым диф
Называется вторым диф
Ференциалом или дифференциалом второго порядка этой функции и обозначается 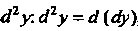 , причем
, причем
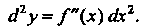 (14.35)
(14.35)
Дифференциалом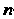 -го порядка называется дифференциал от дифференциала
-го порядка называется дифференциал от дифференциала 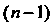 -го порядка:
-го порядка: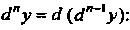
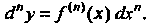 (14.36)
(14.36)
Замечание. Формулы(14.35) и(14.36) при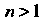 Справедливы, когда
Справедливы, когда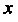 является независимой переменной.
является независимой переменной.
| < Предыдущая | Следующая > |
|---|