14.3. Основные формулы дифференцирования
Производные степенных и тригонометрических функций выражаются следующими формулами:
/
(*“)' = С«а-\ х>1, Ь/*)' = ^=г> ^ =--1,
(8Ш х)' - созх, (созх)' = - зт х,
ДГ X
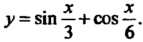
Пример 14.5. Найти производную функции у = 8Ш —н сов —.
3 6
Применяя формулы (14.11), находим
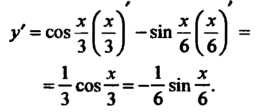
1 х 1.x
~"зС08з --681П б‘
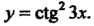
Пример 14.6. Найти производную функции у = с1§2 Зх.
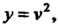
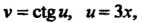
Так как = V2, где V = с\%и, и= Зх, то формулу (14,8) применяем дважды. На основании формулы (14.10) и второй из формул (14.12) получаем
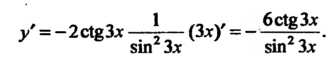
/ = -2с1ёЗх - Л— (Зх)' = -
81П Зх 8Ш Зх
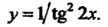
Пример 14.7. Найти производную функции у = 0®2 2х.
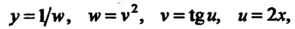
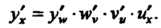
Так как у = \]м/, и» = V2, V = и = 2х, то у' =у{,-и*' • у' •«'. Применяя
Формулу (14.10) и первую из формул (14.12), находим
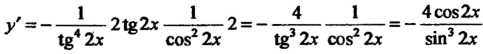
, 1 . - 1 . 4 1 4сов2х
У —--—21®2х-5—2 =--;--г— =--^-.
1%‘ 2х сов 2х 18 2х сов 2х 81П 2х Х л1па
(1п х)' = — (дг>0), (1пЫ)' = — (х Ф 0). х х
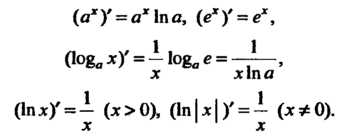
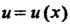
Если и = и (х) - дифференцируемая функция, то
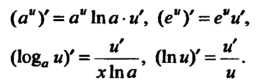
(аи)' = а" 1па-и', (еиу = е“и', (14.13)
(1°8а «У = 0п«)' = -¦ (14.14)
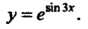
Пример 14.8. Найти производную функции > = е5т3х.
Применяя вторую из формул (14.13), находим
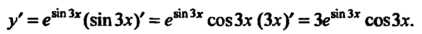
У' = е5т3г($тЗх)' = е81"3* совЗх (Зх)' = Зенп31 сояЗх Пример 14.9. Найти производную функции у = 1п(1+л2). На основании второй из формул (14.14) получаем
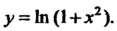
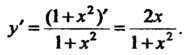
, (1+х2)' 2х
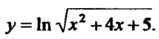
Пример 14.10. Найти производную функции у = 1пл/л2 +4х + 5. Так
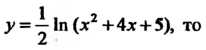
1 1
Как у = — \п(х +4х + 5), то
(*2+4х + 5)' _ х+2 У 2(х2 + 4* + 5) х2 + 4х + 5 Производные обратных тригонометрических функций находят по формулам
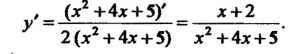
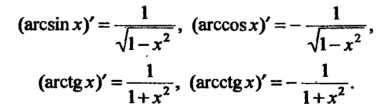
(агсвт х)' = ¦ =¦, (агссозл)' = —. * ,
•\/1-*2 л/1-*2
(агс1ёх)' = —Ц-, (агсс1§*)' = -—Ц-.
\+х 1+хг
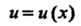
Если и = и (х) — дифференцируемая функция от х, то
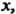
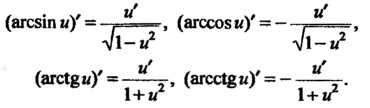
(агс51пм)/= . и (агссок и)' = - , М - , (14.15)
VI-и2 л/1-«2
(ах<Л%и)' = -- , (агсс1§м)' =--(14.16)
1 +и 1 + и
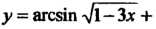
Пример 14.11. Найти производную функции у = агсвт л/1-3* + +агссо$ - Д-2х.
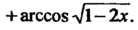
Если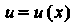 - дифференцируемая функция, то
- дифференцируемая функция, то
(14.17)
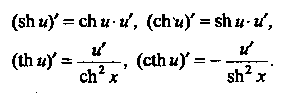 (14.18)
(14.18)
Пример 14.13. Найти производную функции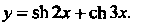 Применяя формулы (14.17), находим
Применяя формулы (14.17), находим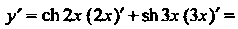
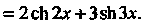
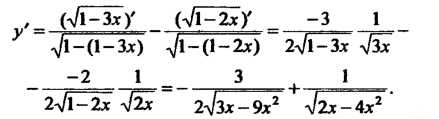
Пример 14.12. Найти производную функции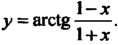 С помощью первой из формул (14.16) и формулы (14.7) получаем
С помощью первой из формул (14.16) и формулы (14.7) получаем
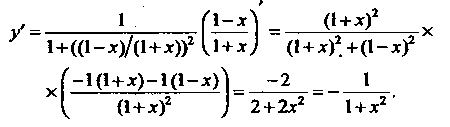
Производные гиперболических функций находят по формулам
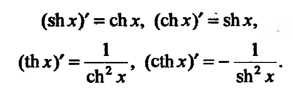
Пример 14.14. Найти производную функции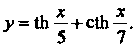 В соответствии с формулами (14.18) получаем
В соответствии с формулами (14.18) получаем
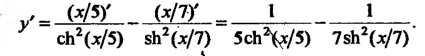
Производные неявных функций и функций, заданных параметрически. Производная функции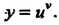 Если дифференцируемая функция
Если дифференцируемая функция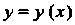 Зада
Зада
На уравнением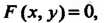 То производная
То производная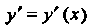 Этой неявной функции
Этой неявной функции
Может быть найдена из уравнения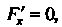 Где
Где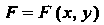 Рассматривается как
Рассматривается как
Сложная функция переменной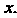
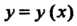
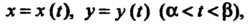
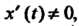
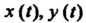
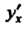
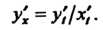
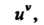
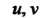
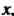
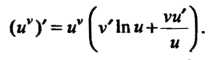
(14.21)
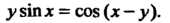
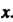

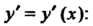
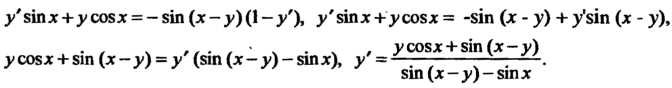
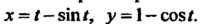
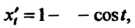
Если функция у = у (х) задана параметрически:
* = *('), У=У(0 (ос<«Р), (14.19) где х ((), у (I) - дифференцируемые функции и х' (_() Ф 0, то ее производная у' определяется формулой
У>У',/х;. (14.20)
Производная степенно-показательной функции и”, где и, V - дифференцируемые функции от х, находится с помощью предварительного логарифмирования, которое приводит к формуле
(ку), = ну^'1пи
Пример 14.15. Найти производную функции, заданной уравнением у8тх = со8(х-у).
Это уравнение определяет у = у (х) — функцию от х. Подставляя функцию у = у (х) в данное уравнение, получаем тождество у (х)втх = сов (х - у (х)). Дифференцируем это тождество и из полученного уравнения находим у' = у' (х): у'зтх + у со$х = - кт (х - у) (1 - у'), у'втх+усовх = -$№ (х - у) + у'кт (х - у),
. • ч, УС08Х + 81П (X-V) у С08 X + 31П (х — У) — У (81П (х — у) — Б1П х), у --.
81П (X — у) — 81П X
Пример 14.16. Найти производную функции, заданной уравнениями х = /-вт/, у = 1-со8/.
Эта функция задана параметрически (см. (14.19)). Так как х,' = 1 - - сов/,
У', = 8ШI, то по формуле (14.20) получаем у' = — =
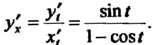
Х\ 1-сок/
Пример 14.17. Найти производную функции у = хыпг.
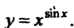
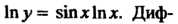
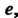
Логарифмируя это равенство по основанию е, получаем 1пу= зшх1пх. Дифференцируя, находим у'/у = С08х1пх + 8тх(1/х), откуда у' = = у (со8х 1пх + втх ¦ (1/х)), у' = хм"х (со8х1пх+втх/х).
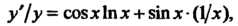
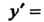
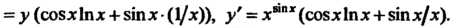
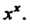
Пример 14.18. Найти производную функции х*.
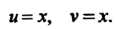
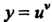
Это также функция у = «у, где и = х, у=х. По формуле (14.21) получаем у' = х*(1пх + 1).
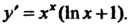
Производные высших порядков. Производной второго порядка, или второй производной, функции у = /(х) называется производная от ее производной у' = /'(х) (которую называют первой производной).
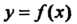
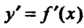
Обозначения второй производной:
У" = (/)', /"(*)=(/'(*))', ^Т = ^Г-
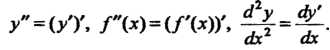
Дх ах
Механический смысл второй производной. Если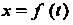 - закон прямолинейного движения точки, то
- закон прямолинейного движения точки, то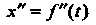 - ускорение этого дви
- ускорение этого дви
Жения в момент времени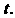
Аналогично определяются и обозначаются производные третьего, четвертого и более высоких порядков:
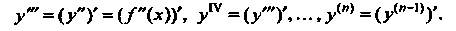
Производная л-го порядка обозначается и так:
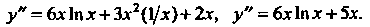
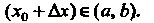
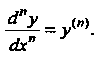
Если функция задана параметрически: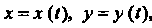 То ее вторая произ
То ее вторая произ
Водная определяется формулой
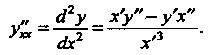 (14.22)
(14.22)
Пример 14.19. Найти вторую производную функции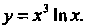
Так как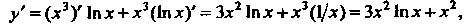 То
То
Пример 14.20. Найти вторую производную функции, заданной параметрически: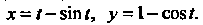
Поскольку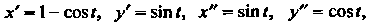 То по формуле (14.22)
То по формуле (14.22)
Получаем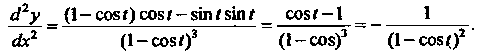
Пример 14.21. Найти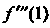 Для функции
Для функции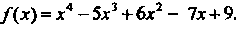
Так как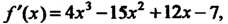
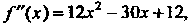 То
То
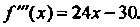 Следовательно,
Следовательно,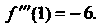
| < Предыдущая | Следующая > |
|---|