14.2. Основные правила дифференцирования

Производная алгебраической суммы функций выражается следующей теоремой.

Теорема 14.2. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

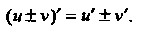(14.5)

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,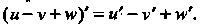

Производную произведения функций определяет

Теорема 14.3. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.

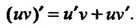(14.6)

Следствие 1. Постоянный множитель можно выносить за знак производной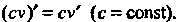

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные. Например,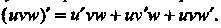

Производная частного двух функций выражается следующей теоремой.

Теорема 14.4. Производная частного двух дифференцируемых функций определяется формулой

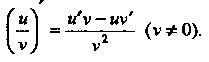
(14.7)

Производную сложной функции выражает

Теорема 14.5. Если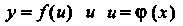— дифференцируемые функции

Своих аргументов, то производная сложной функции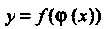Существует и

Равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.

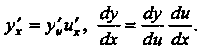(14.8)

Производная обратной функции. Бели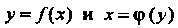- взаимно об

Ратные дифференцируемые функции и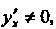То

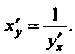(14.9)

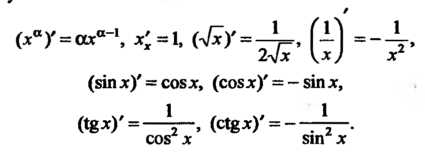
Если и=и(х) - дифференцируемая функция, то

(*8*)' =—Т~> («8*)' =—•

С08 X  81П X

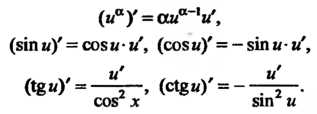
Пример 14.4. Найти производную функции у = -^1-х2.

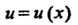
(иау = аиа~'и\  (14.10)

(8ти)' = со8и и', (со81/)' = -8Шм м',  (14.11)

(18«)' = -^-, (с18«,)' = --4-.  (14.12)

С05 X  81П и

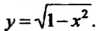
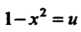
Считая 1-х2 = и и применяя формулу (14.10), получаем

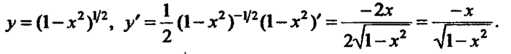
, = (1-*У\ / = 1(1-^)-|/2(1-^У= ^г =

< Предыдущая		Следующая >