13.11. Показательная функция. Гиперболические функции
Показательной (экспоненциальной) называется функция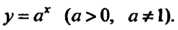
Пусть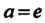
(см. формулу 13.18), в этом случае показательная (экспоненциальная) функция обозначается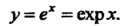
Показательную функцию с другим основанием можно привести к показательной функции с основанием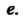
Действительно, по определению логарифма 
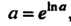, поэтому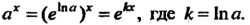
Гиперболическим синусом называется функция, определяемая формулой
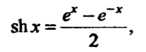(13.26)
Гиперболическим косинусом - функция
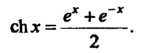(13.27)
Гиперболический тангенс и гиперболический котангенс определяются соответственно формулами
(13.28)
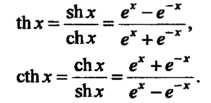(13.29)
Функции, определяемые формулами (13.26) - (13.29), называются ги перболичес кими.
Гиперболические функции имеют вполне определенные значения при всех значениях х, кроме функции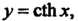
Которая в точке
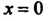Обращается в бесконечность. Отметим, что
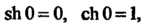Как и для обычных синуса и косинуса.
Гиперболические функции не обладают важнейшим свойством тригонометрических функций - свойством периодичности. Кроме того, множество значений
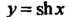
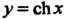
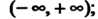
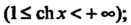
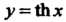
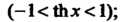
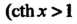
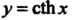
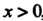
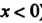
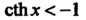
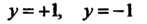
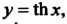
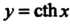
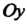
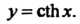
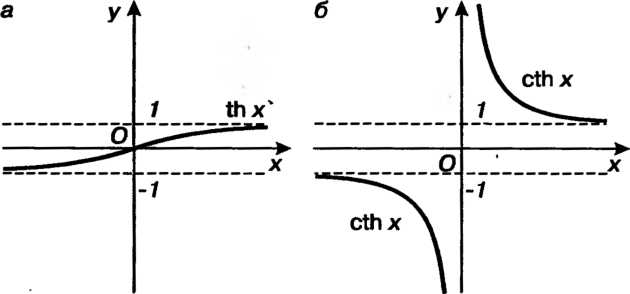
Каждой гиперболической функции существенно отличается от множества значений соответствующей тригонометрической функции. Функция у = хЬх принимает все действительные значения, т. е. множество ее значений совпадает с бесконечным интервалом (—+ у = с\\х - значения, не меньше единицы (1^сЬх< + ~); значения функции у — 1Ьх по модулю не превышают единицы (-1<&х<1); значения у = сЛх по модулю больше единицы (сЙ1 х > 1 при х>0, сЙ1х<-1 прих<0).
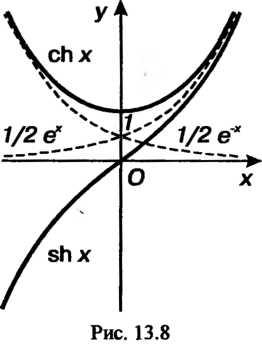
Графики гиперболических функций представлены на рис. 13.8 и 13.9, я, б. Прямые у = +1, у = — 1 являются асимптотами графиков функций у = Й1 х, у = сЙ1х. Кроме того, ось Оу служит асимптотой графика функции у - с1Ьх.
| < Предыдущая | Следующая > |
|---|
