13.10. Точки разрыва функции
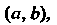
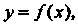
Рассмотрим функцию у = /(х), определенную на интервале (а, Ь), кроме, быть может, точки х0 е (о, Ь). Значение аргумента х0 называется точкой разрыва данной функции, если при х = х0 функция определена, но не является непрерывной или ие определена при этом значении х.
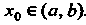
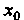
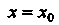
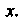
Если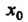 — точка разрыва
— точка разрыва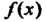 И существуют конечные пределы
И существуют конечные пределы
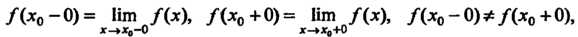 То она называется точкой разрыва первого рода. Величина
То она называется точкой разрыва первого рода. Величина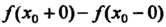 Называется скачком функции
Называется скачком функции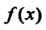 В точке
В точке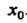
Если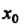 — точка разрыва и
— точка разрыва и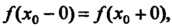 То
То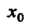 Называется точкой
Называется точкой
Устранимого разрыва.
Если хотя бы один из односторонних пределов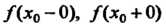 Не существует
Не существует
Или является бесконечным, то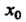 Называется точкой разрыва второго рода.
Называется точкой разрыва второго рода.
Пример 13.18. Функция 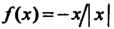 В точке
В точке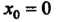 Имеет
Имеет
Разрыв первого рода.
Действительно,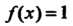 При
При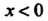
И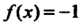 При
При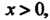 В точке
В точке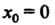
Функция не определена;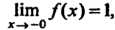
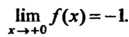 Скачок функции в точ
Скачок функции в точ
Ке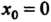 Равен
Равен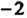 (рис. 13.5).
(рис. 13.5).
Пример 13.19. Для функции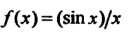 Значение аргумента
Значение аргумента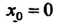
Является точкой устранимого разрыва.
В самом деле, при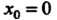 Данная функция не определена, ио имеет равные од
Данная функция не определена, ио имеет равные од
Носторонние пределы:
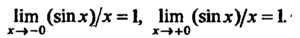
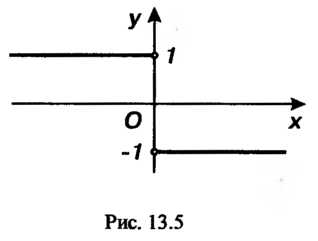
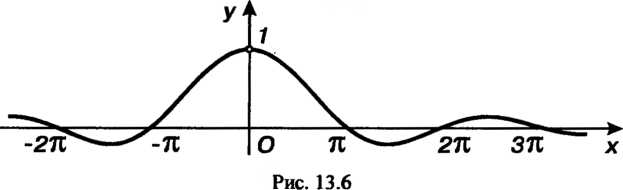
График функции изображен на рис. 13.6.
Пример 13.20. Функция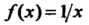 В точке
В точке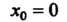 Имеет разрыв
Имеет разрыв
Второго рода, так как
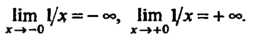
Пример 13.21. Для функции
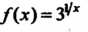 Значение
Значение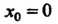 Является
Является
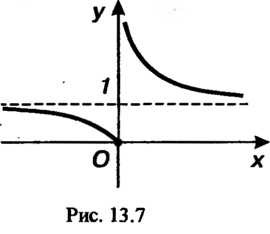
Точкой разрыва второго рода, так как
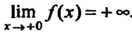 . Второй односторонний
. Второй односторонний
Предел конечен: (рис. 13.7).
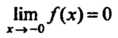
| < Предыдущая | Следующая > |
|---|