13.09. Непрерывность функции

 

Функция у = /(*), определенная иа интервале (а, Ь), называется непрерывной в точке х0 е (а, Ь), если

Нт /(*) = /(*„)  (13.24)

(т. е. предел функции равен ее значению при предельном значении аргумента). Согласно определению предела функции, условие (13.24) равносильно следующему: для любого числа е>0 существует такое число 6 > 0, что при всех х, удовлетворяющих условию 0 < | х - а | < 6, выполняется неравенство | /(*)-/(*0)| < е.

Если х0 6 (а, Ь) и х е (а, Ь), то разность Ах = х-х0 называется приращением аргумента в точке х0, а разность Ау = /(х)- /(х0), или Ау = /(х0 + Дх)-/(х0), - приращением функции в той же точке (рис. 13.1); Ау - функция Ах.

Необходимое и достаточное условие непрерывности функции у = /(х) в точке х0 выра

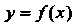
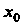
Жается равенством

 

(13.25)

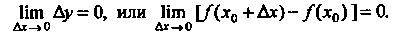
Итак, функция непрерывна в точке, если бесконечно малому приращению аргумента в этой точке соответствует бесконечно малое приращение функции.

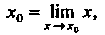
Замечание. Поскольку х0 = Нт х, то формулу (13.24) можно перепи-

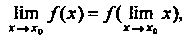
Сать так: Нт /(х) = /( Нт х), т. е. для непрерывной функции символы предела и

Х-*х0

Функции перестановочны.

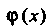
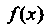
Теорема 13.12. Если функции /(х) и <р(х) непрерывны в точке х0, то

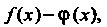
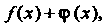
Также непрерывны в этой точке их сумма /(х)+<р(х), разность /(х)-ф(х),

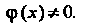
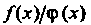
Произведение /(х)<р(х), а также частное /(х)/<р(х) при условии, что <р(х)*0.

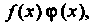
Следствие 1. Целая рациональная функция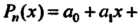 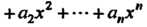Непрерывна при всех Следствие 2. Дробная рациональная функция

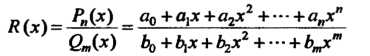
Непрерывна при всех х, для которых знаменатель не обращается в нуль.

Теорема 13.13. Если функция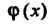Непрерывна в точке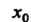, а функция

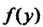Непрерывна в точке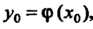То сложная функция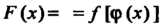

Непрерывна в точке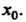

Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.

Если функция определена при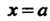И при этом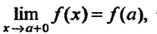То говорят,

Что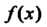В точке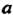Непрерывна справа. Аналогично, если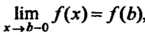, то

Говорят, что в точке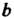Эта функция непрерывна слева.

Функция называется непрерывной иа отрезке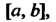Если она непрерывна в

Каждой его точке (в точке а - непрерывна справа, в точке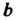- непрерывна слева).

Отметим, что основные элементарные функции непрерывны в соответствующей области определения.

Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.

Теорема 13.14. Функция, непрерывная на отрезке _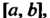_ достигает в нем своего

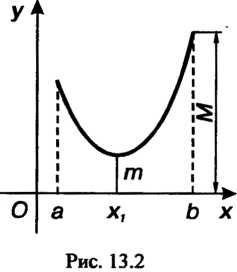
Наименьшего значения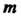И наибольшего значения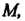Т. е. существуют такие точки 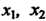этого отрезка, что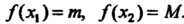

Эта теорема имеет простой геометрический смысл (рис. 13.2).

Замечание. Функция, непрерывная на интервале, этим свойством не обладает.

Например, функция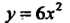На интервале

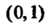Не достигает значени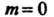йИ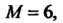

Так как эти значения функция принимает в точках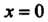И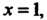А последние данному интервалу не принадлежат.

Теорема 13.15. Если функция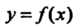Непрерывна на отрезке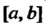

И на его концах принимает неравные значения

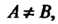То каково бы ни было число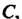. заключенное между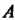И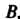 найдется точка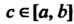Такая, что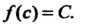

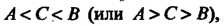
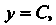
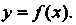
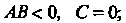
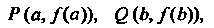
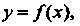
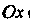
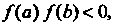
Геометрический смысл теоремы иллюстрируется на рис. 13.3, а, б. Всякая прямая у = С, где А < С< В (или А>С>В), пересекает график функции у — /(*).

Следствие. Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке найдется хотя бы одна точка, в которой функция обращается в нуль.

Это частный случай теоремы: АВ< О, С = 0; геометрический смысл: 1рафик непрерывной фуйкции у = /(х), соединяющий точки Р(а,/(а)), для которых /(а) /(Ь) < 0, пересекает ось Ох (рис. 13.4, а, б).

Отметим, что сумма конечного числа функций, непрерывных на некотором отрезке, непрерывна на этом отрезке.

Рис. 13.3

< Предыдущая		Следующая >