13.07.  Основные теоремы о пределах функций

 

Теорема 13.8. Функция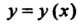Не может иметь более одного

Предела при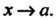

Теорема 13.9. Пусть функция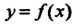Определена в некотором проме

Жутке, содержащем точку а. Если при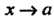Функция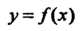Имеет поло

Жительный (отрицательный) предел, то найдется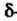-окрестность точки а такая, что для всех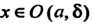Функция положительна (отрицательна).

Эта теорема называется теоремой о сохранении знака функции, имеющей предел.

Теорема 13.10. Если функции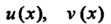Определены в некоторой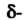

Окрестности точки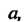Для всех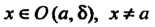Выполняется неравенство

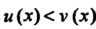И функции имеют пределы при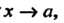То

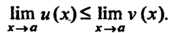
Замечание. Теорему 13.10 кратко можно сформулировать так: в неравенстве, обе части которого имеют пределы, можно перейти к пределу, присоединив зиак равенства. Например,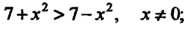

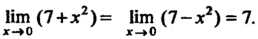
Теорема 13.11. Пусть три функции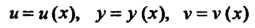Опреде

Лены в некотором промежутке, содержащем точку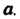

Еслидля любого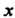Из этого промежутка выполняются неравенства 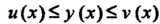И функции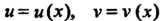Имеют одинаковые пределы

При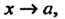То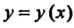Имеет тот же предел при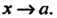

< Предыдущая		Следующая >