13.06. Бесконечно большие функции
Функция у = /(х) называется бесконечно большой при х -» а, если для любого положительного числа N можно найти такое число 6 > 0, что при всех значениях х, удовлетворяющих условию 0 < | х - а | < 6, выполняется неравенство | /(*) | > N.
Бесконечно большая функция не имеет предела при х -» а, но иногда условно говорят, что ее предел равен бесконечности, и пишут: Нт /(*) = “, или
Х—*а
/(х) -» оо, при х -» а.
Если /(*) стремится к бесконечности при х -» а, принимая только положительные или только отрицательные значения, то соответственно пишут: Нт /(х) = + оо, Нт /(*) = — оо.
Х—*а х—*а
Если функция /(х) стремится к бесконечности при х-»оо; то пишут Нт /(х) = оо.
X—» “
Примером бесконечно большой функции является функция /(*)= 1/* при х -»0. В самом деле, при любом N>0 неравенство \Уx\>N будет выполнено,
Так как
Х5 х
Нт —-г— = Нт-5- = О,
(2+х) *-*о2+*
То функция а(х) = х5/(2+х2) есть бесконечно малая высшего порядка, чем функция р(х) = дЛ
Пример 13.10. Найти Нт —5-.
*->зх2-5х + 6
При х—>3 функции х-3, 81п (х — 3) являются эквивалентными бесконечно малыми. Поскольку при замене бесконечно малой функции $т(д:-3) эквивалентной ей функцией х-3 предел отношения не изменится, то Цт ап (х-3) =Нт зт(*-3) =
*->3х -5х + 6 *->3 (х-3)(х-2)
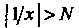
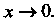
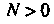
Если _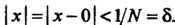 | Эта функция принимает положительные значения при
| Эта функция принимает положительные значения при
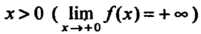 И отрицательные - при
И отрицательные - при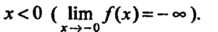
Функция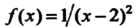 - бесконечно большая при
- бесконечно большая при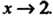 Действительно,
Действительно,
При любом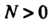 Неравенство
Неравенство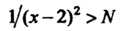 Будет выполнено, если
Будет выполнено, если
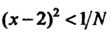 Или
Или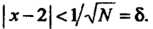 Данная функция принимает только положи
Данная функция принимает только положи
Тельные значения.
Если функция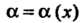 Стремится к нулю при
Стремится к нулю при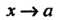 (или
(или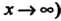 И не обра
И не обра
Щается в нуль, то функция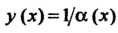 Стремится к бесконечности.
Стремится к бесконечности.
| < Предыдущая | Следующая > |
|---|