13.05. Сравнение бесконечно малых функций
Бесконечно малые а (х) и р (х) при х —»а называются величинами одного порядка, если их отношение имеет конечный предел, отличный от нуля, т. е.
.. а(х) Р(х) 1 ,
Нт ¦ — с, или Нт - = — (с Ф 0).
*-»°р(х) *-><>а(х) с
В этом случае пишут: а (д;) = 0 (р (х)) при х -» а (читается: а (х) есть О большое от р (х) при х-*а).
Например, а(х) = 8Шх и р (х) = Зх при х-»0 являются бесконечно малыми одного порядка, так как Нт а(х)/р(х) = 1/3, зтх = 0(3х) при х 0.
Х-»0
Если предел отношения а (х)/р (х) при х -» а равен нулю (с = 0), то величина а (х) называется бесконечно малой высшего порядка по сравнению с Р (х) (величина р (х) - бесконечно малая низшего порядка по сравнению с а (х) ). В данном случае применяется обозначение а(х) = о(Р(х)) при х —» а (читается: а(х) есть о малое от р (х) при х -» а ). Например, х2 = о (зт х) при х —» 0, поскольку
Х2 х
Нт-= Нт х Нт-= 0-1 = 0.
*-*0 31ПХ *-»0 х-»0 51ПХ
Функция р (х) называется бесконечно малой к-го порядка относительно функции а(х), если р(х) и (а(х))* - бесконечно малые одного порядка, т. е.
Нт = с (с* 0).
— («(*))*
Например, если а(х) = х, р(х) = х4, то при х —> 0 Р(х) - бесконечно малая четвертого порядка относительно бесконечно малой а(х) (но бесконечно малая второго порядка по сравнению с у (х) = х2).
Две бесконечно малые функции а(х) и р(х) называются эквивалентными (или равносильными) бесконечно малыми при х -» а, если предел их отношения равен единице, т. е.
Нт — - = 1, или Нт =1. х~*а р(х) *->“а(х)
Эквивалентность бесконечно малых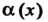 И
И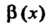 Обозначается символом -
Обозначается символом -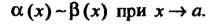 Из формул (13.17) и (13.22) (см. п. 13.8) следует, что при
Из формул (13.17) и (13.22) (см. п. 13.8) следует, что при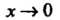
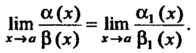
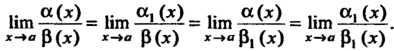
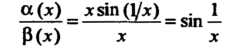
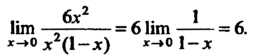
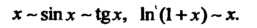
Теорема 13.6. Бесконечно малые функции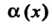 И
И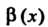 Эквивалентны тогда и только тогда, когда их разность есть бесконечно малая высшего порядка по сравнению с каждой из них.
Эквивалентны тогда и только тогда, когда их разность есть бесконечно малая высшего порядка по сравнению с каждой из них.
Теорема 13.7. Если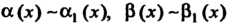 При
При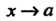 И существует
И существует
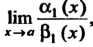 , то существует
, то существует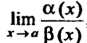 , причем
, причем
Следствие. Если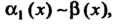
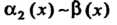 При
При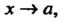 То
То
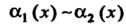 При
При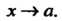
При нахождении предела отношения двух бесконечно малых функций каждую из них (или только одну) можно заменить другой бесконечно малой, ей эквивалентной: если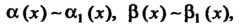 То
То
Замечание. Если отношение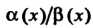 Двух бесконечно малых
Двух бесконечно малых
Функций при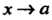 Не имеет предела и не стремится к бесконечности, то беско
Не имеет предела и не стремится к бесконечности, то беско
Нечно малые функции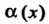 И
И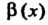 Несравнимы между собой. Например, несравнимы при
Несравнимы между собой. Например, несравнимы при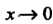 Бесконечно малые функции
Бесконечно малые функции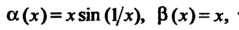 Гак как
Гак как
И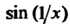 Не имеет предела при
Не имеет предела при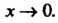
Пример 13.8. Доказать, что функции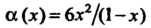 Н
Н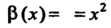
При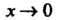 Являются бесконечно малыми одного порядка.
Являются бесконечно малыми одного порядка.
Найдем предел отношения двух данных функций:
Поскольку полученный предел отличен от нуля, то данные функции являются бесконечно малыми одного порядка.
Пример!3.9. Доказать, что порядок функции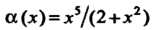 Выше,
Выше,
Чем порядок функции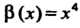 При
При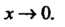
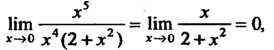
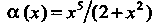
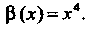
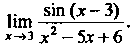
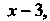
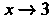
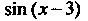
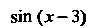
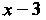
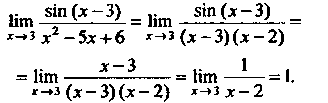
= Нт--—--= Нт —-— = 1.
*-»з (х-3)(л:-2) х — 2
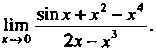
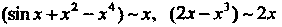
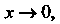
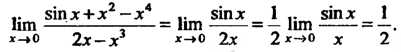
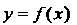
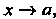
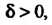
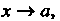
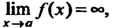
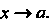
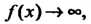
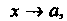
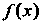
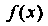
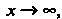
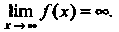
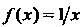
Пример 13.11. Найти Нт 5‘п*+* х.
*-»о 2х-х3
Так как (втх+х2 - х4)~х, (2х-х3)~2х при х-*0, то
Зтх+х2 - хл 8ШДГ 1 .. 8шдг 1
Пт —:-5-= пт-= — »т-= —.
*->о 2х-х х->° 2х 2*->о х 2
| < Предыдущая | Следующая > |
|---|