13.04. Бесконечно малые функции и их свойства
Функция а = а (дс) называется бесконечно малой при х -» а (илн при х —у “), если ее предел равен нулю:
Нт а (дс) = О ( Нт а (дг) = 0).
Х—>о
Например, функция а (дс) = (дг-5)2 есть бесконечно малая при х -» 5, так как Иша(х)= Нт (х-5)2 = 0; функция а(дс) = 1/дс является бесконечно малой при
Х->5 х—> 5 *
Х -» о», поскольку
Нт а (дс) = 1йп — = 0.
Х-*- *->- X
Принимая во внимание определение предела функции, определение бесконечно малой функции можно сформулировать следующим образом.
Функция а = а (дс) называется бесконечно малой при х -> а, если, задав любое число е > 0, можно указать такое число 6 > 0, что для всех х, удовлетворяющих условию 0 < | х - а | < 6, выполняется неравенство | о. (х) | < е.
Свойства бесконечно малых выражаются следующими теоремами.
Теорема 13.3. Если функция у = .у(дс) имеет предел Ь при х—*а, то
У(х) = Ь+а.(х), у = Ь+а, (13.16)
Где а = а (дс) - бесконечно малая при х —» а. Обратное также верно: если выполнено равенство (13.16), то Нту(х)=6.
X —
Теорема 13.4. Алгебраическая сумма конечного числа бесконечно малых функций при ха есть бесконечно малая функция при х-* а.
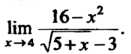
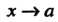
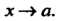
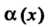
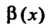
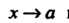

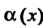
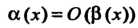
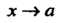
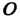
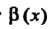
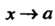
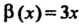
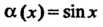
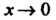
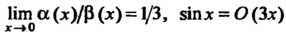
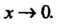
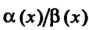
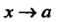
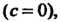
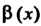
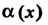
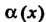
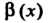
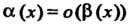
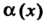
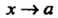
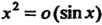
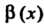
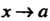
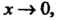
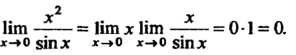
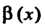
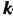
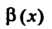
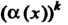
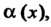
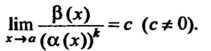
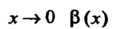
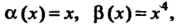
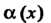
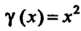
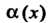
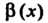
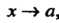
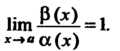
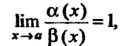
Теорема 13.5. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.
Следствие 1. Произведение двух бесконечно малых функций есть бесконечно малая функция.
Следствие 2. Произведение бесконечно малой функции на постоянную есть бесконечно малая функция.
| < Предыдущая | Следующая > |
|---|