13.03. Предел функции

 

Постоянная Ь называется пределом функции у = /(х) при х -» а (или в точке в), если для любого числа е > 0 существует такое число 6 > 0, что при всех х, удовлетворяющих условию

О < | х - а | < 8,

Выполняется неравенство

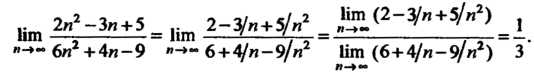
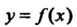
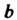
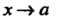
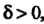
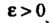
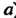
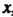
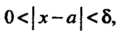
|/(х)-Ь|<е.

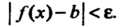
Нт /(х)=Ь; /(х)-> Ь при х-*а.

Х—*а

 

Предел функции /(*) при х, стремящемся к а, обозначают:

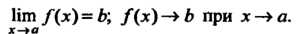
Рассматривают также односторонние пределы функций: предел слева Нт /(х) = 6, (л: стремится к о, оставаясь меньше а; х<а) и предел справа

Х-»о-0

Нт /(х) = ^ (х стремится к а, оставаясь больше а; х> а). Если односторонние пре-

Х-*а+0

Делы равны: Нт /(х) = Нт /(х) = Ь, то предел функции /(х) в точке а существу-

Х-»а-0  х-»а+0

Ет и равен Ь: Нт /(х) = 6. Если односторонние пределы различны или хотя бы один из

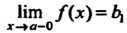
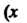
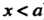
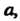
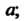
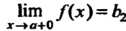
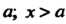
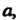
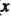
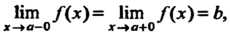
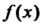
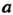
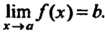
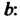
Них не существует, то не существует и предел функции в соответствующей точке.

Если с - постоянная величина, то Нт с = с.

Х-*а

Если функции /(х) и <р (х) имеют пределы при х - у а, то

Нт (/(х)±<р(х))= Нт /(х)± Нт ф(х),  (13.9)

Х-*а  х->а  х-*а

Нт (/(х)ф(х))= Нт /(х) Нт ф(х),  (13.10)

Х—*а  х-*а  х—*а

Ит

Ц= - ( Нт ф (х) * 0).  (13.11)

'-*“'ф(х) Нтф(х)

Х->а

Из (13.10) следует, что

Нт (с/(х))= с Нт /(х) (с = сопй),  (13.12)

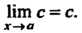
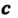
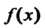
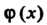
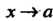
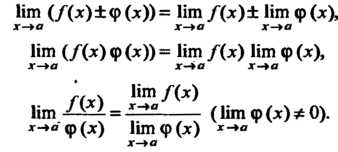
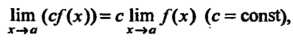
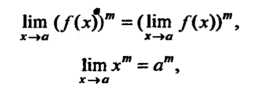
Ига (Дл)У = (Нт Дл))и,  (13.13)

 

Нтлт = ат,  (13.14)

Х—

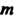
Где /л — натуральное число.

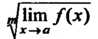
Если ™/Пт /(х) существует, то

*\х-ю

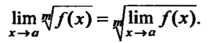
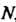
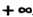
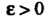
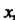
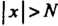
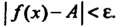
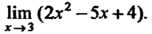
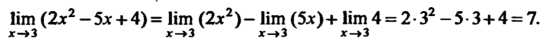
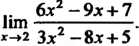
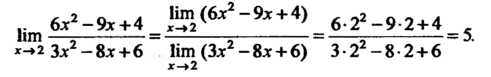
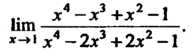
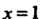
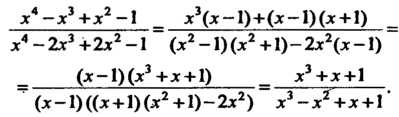
Нт ^Дх) = МкпДх).  (13.15)

Х-»а  ух-»а

Число А называется пределом функции. у = /(х) при л, стремящемся к — «> или + «*>, если для любого числа е > 0 можно указать положительное число ТУ, такое, что при всех значениях х, удовлетворяющих условию | л | > N, выполнялось неравенство | Дл) - А | < е.

Пример 13.4.Найти Нт (2х2 -5* + 4).

Х->3

Применяя формулы (13.9), (13.12), (13.14), получаем

Нт (2л2-5л+ 4)= Нт (2л2)- Нт (5л)+ Нт4 = 2-32 -53+4 = 7.

Х—>3  х —> 3  х—>3  х—>3

_  ТТ „ .. 6л2-9л+ 7

Пример 13.5. Наити 1ип—;-.

*-»* Зл - 8л + 5

С помощью формулы (13.11) и формул, указанных в примере 13.4, находим

Ит 6л2-9л+4 ]™(6д2~9:,С + 4)_ 6-22-9-2 + 4_5 *-»* Зл2-8л+6 Нт (Зл2-8л + 6) 3-22-8-2+6

Х—>2

Л4-л3+л2-1

Пример 13.6. Нт —-г——г—.

*-*• л4-2л3+2л2-1

При х = 1 числитель и знаменатель дроби равны нулю, имеем неопределенность вида Ц. Чтобы раскрыть ее, предварительно преобразуем данную дробь, разложив многочлены на множители:

Л4—л3+л2—1 _ х3(х — 1)+(л — 1)(л + 1) _ л4—2л3+2л2—1 “ (л2-1)(л2 +1)-2л2(л-1)“

(л —1)(л3 + л + 1) _ л3 +л+1 ~ (л —1)((л+1)(л2+1)—2л2) л3-л2+л + Г. Переходя к пределу, получаем

.. л4—л3+л2-1 .. л3+л + 1 3 Нт ----— = Нт -  —

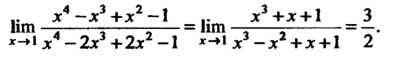
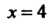
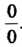
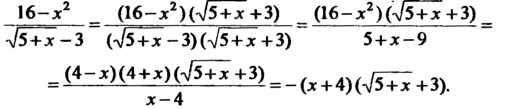
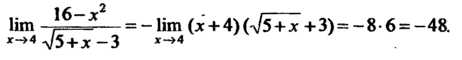
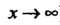
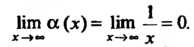
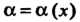
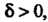
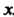
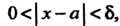
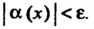
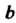
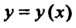
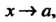
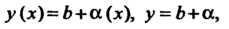
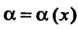
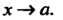
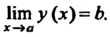
*->« л/5+х-З

При х = 4 числитель н знаменатель дроби обращаются в нуль, имеем неопределенность вида - Ц. Чтобы раскрыть эту неопределенность, предварительно преобразуем дробь:

16-*2 = (16-*2) (л/5+7+3) (16 - ^с2) (л/5+7+ 3)^ л/5+.х—3 (л/5+7^- 3) (л/ 5+х +3)  5+дг-9

= (4-?)(4+/)(^+1±3) = -(х+4)(^+3).

Х-4

Переходя к пределу с использованием формулы (13.15), находим

Пт ~т-=Л— = - Пт (дг + 4)(л/5+дг +3)=-8 6 = -48.

«-»4л/ 5+дс-З *-»4

 

< Предыдущая		Следующая >