13.02. Предел последовательности
Числовой последовательностью (или последовательностью) называется функция
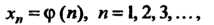
Определенная на множестве натуральных чисел. Каждое значение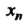
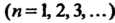 Называется элементом последовательности, а число
Называется элементом последовательности, а число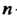 - его номером.
- его номером.
Числовую последовательность с элементом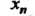 Обозначают либо
Обозначают либо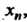
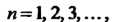 Либо
Либо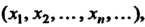 Либо
Либо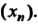
Примеры числовых последовательностей: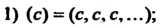
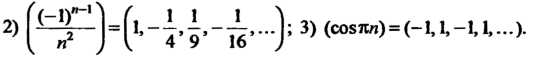
Числовая последовательность всегда содержит бесконечное множество элементов; среди них могут быть равные (см. примеры 1) и 3))-
Число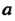 Называется пределом последовательности
Называется пределом последовательности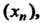 Если для любого числа
Если для любого числа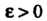 Найдется такое натуральное число
Найдется такое натуральное число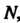 Что при всех
Что при всех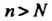 Выполняется неравенство
Выполняется неравенство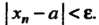
Предел последовательности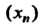 Обозначают
Обозначают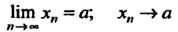 При
При
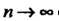 (читается:
(читается: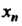 Стремится к
Стремится к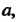 Когда
Когда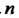 Стремится к бесконечности).
Стремится к бесконечности).
Последовательность, имеющая предел, называется сходящейся. Последовательность, у которой нет предела, называется расходящейся.
Интервал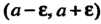 Называется
Называется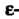 Окрестностью точки о и обозначается
Окрестностью точки о и обозначается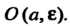
Определение предела имеет следующий геометрический смысл: число а является пределом последовательности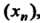 , если в любой его е-окрестности содержатся почти все члены
, если в любой его е-окрестности содержатся почти все члены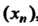 , или вне этой окрестности находится лишь конечное число членов данной последовательности.
, или вне этой окрестности находится лишь конечное число членов данной последовательности.
Из определения предела последовательности следует, что предел постоянной равен этой постоянной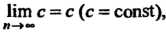 Поскольку в данном случае
Поскольку в данном случае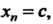
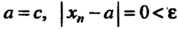 Для любого
Для любого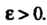 Из определения следует также, что по
Из определения следует также, что по
Следовательность может иметь только один предел.
Последовательность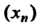 Называется ограниченной сверху (снизу), если существует такое число
Называется ограниченной сверху (снизу), если существует такое число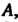 Что
Что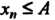 (соответственно
(соответственно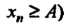 Для всех номеров
Для всех номеров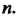
Последовательность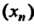 , ограниченная сверху и снизу, называется просто ограниченной.
, ограниченная сверху и снизу, называется просто ограниченной.
Очевидно, последовательность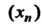 Мраничена тогда и только тогда, когда существует такое число
Мраничена тогда и только тогда, когда существует такое число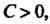 Что
Что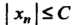 Для всех номеров п.
Для всех номеров п.
Например, последовательности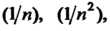
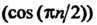 Ограничены, после
Ограничены, после
Довательность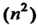 Ограничена снизу, но не ограничена сверху, последовательность (и cos ли) не является ограниченной ни сверху, ни снизу.
Ограничена снизу, но не ограничена сверху, последовательность (и cos ли) не является ограниченной ни сверху, ни снизу.
Теорема 13.1. Если последовательность имеет предел, то она ограничена
Число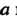 Называется верхней гранью последовательности
Называется верхней гранью последовательности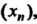 Если: 1)
Если: 1)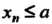 при всех
при всех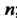 ; 2) для любого
; 2) для любого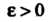 Существует такой номер
Существует такой номер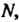 Что
Что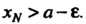 .Верх
.Верх
Няя грань последовательности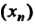 Обозначается
Обозначается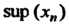 Или
Или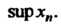
Аналогично определяется нижняя грань последовательности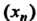 И обозначается
И обозначается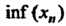 Или
Или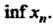
В качестве примеров отметим, что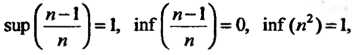
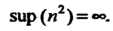
Последовательность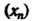 Называется монотонно возрастающей (монотонно убывающей), если
Называется монотонно возрастающей (монотонно убывающей), если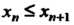 (соответственно
(соответственно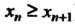 ) при всех
) при всех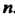 , Монотонно возрастающие или монотонно убывающие последовательности называются просто монотонными.
, Монотонно возрастающие или монотонно убывающие последовательности называются просто монотонными.
Теорема 13.2. Всякая ограниченная сверху (снизу) монотонно возрастающая (.монотонно убывающая) последовательность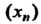 Имеет предел, причем
Имеет предел, причем
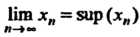 (соответственно
(соответственно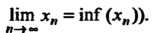
Если последовательности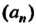 И
И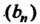 Имеют пределы, то пределы их суммы, разности, произведения, частного существуют и находятся по формулам
Имеют пределы, то пределы их суммы, разности, произведения, частного существуют и находятся по формулам
(13.4)
(13.5)
(13.6)
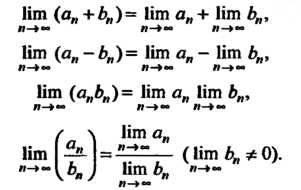 (13.7)
(13.7)
Пример 13.1. Последовательность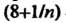 Сходится и имеет предел
Сходится и имеет предел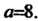
Действительно, каково бы ни было число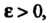 Найдется такое натураль
Найдется такое натураль
Ное число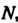 , что
, что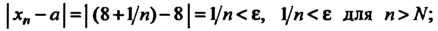 Неравен
Неравен
Ство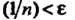 Будет выполнено при всех
Будет выполнено при всех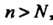 Если
Если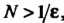 , т. е. в качестве
, т. е. в качестве
N можно взять большее из двух последовательных натуральных чисел, между которыми заключено число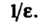 Например, если
Например, если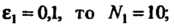 Если
Если
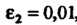 , то
, то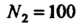 Ит. д.
Ит. д.
Замечание. Одновременно показано, что последовательность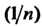 имеет пределом нуль, т. е.
имеет пределом нуль, т. е.
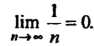 (13.8)
(13.8)
Пример 13.2. Последовательность Является расходящейся.
Является расходящейся.
В самом деле, каково бы ни было число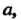 Вне его
Вне его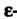 Окрестности, например при
Окрестности, например при 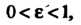 Заведомо лежит бесконечное множество элементов данной последовательности (хотя среди них и много равных между собой); это означает, что
Заведомо лежит бесконечное множество элементов данной последовательности (хотя среди них и много равных между собой); это означает, что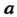 Не является ее пределом.
Не является ее пределом.
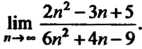
Пример 13.3. Найти Нт + ^.
«-*“ 6и +4п-9
Разделив числитель и знаменатель дроби на п2 и применив формулы (13.4) — (13.8), получим
- 2 э « о о/ </2 Нт (2 — 3/и +5/я2) ,
Вт 2-У3-” + 5 = Нт = — -_=
И*->вв 6и + 4л-9 6 + 4/л-9/л Пт (6+4/л-9/л ) 3
И—»“
| < Предыдущая | Следующая > |
|---|