13.01. Понятие функции. Основные определения

 

Рассмотрим множество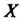Элементов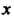И множество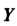Элементов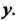Если каждому элементу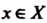По определенному правилу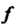Поставлен в соответствие единственный элемент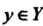, то говорят, что на множестве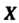Задана функция 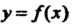Со значениями в множестве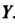. Элементы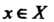Называются значениями аргумента, а элементы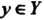— значениями функции. Множество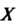Называют областью определения функции, множество всех значений функции - областью значений этой функции.

Замечание. Функцию, заданную на множестве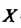Со значениями в множестве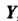, называют также отображением множества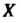В множество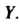Если множество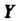Является множеством значений функции, торассматриваемую функцию называют отображением множества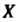На множество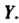

Функцию, заданную на множестве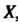, называют также оператором, заданным на множестве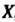, и обозначают символом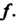

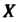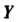В случае, когдаИ— числовые множества, соответствующие функции называются числовыми функциями. Если рассматриваются действительные числа, то функции называют действительными (вещественными) функциями одной действительной (вещественной) переменной.

Употребляются следующие обозначения функции: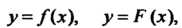

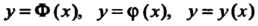И т. п. Значение, которое функция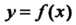При

Нимает при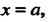Обозначается через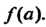

Функция и аргумент могут обозначатся также другими буквами, например

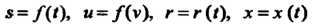И т. д.

К простейшим областям определения функции относятся отрезок, интервал, полуинтервалы или совокупность указанных промежутков. Например, для функции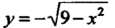Областью определения является отрезок 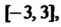А областью ее значений - отрезок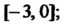Для функции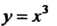Область определения и область значений совпадают с интервалом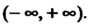

Графиком функции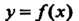Называется множество точек плоскости, коорди

Наты которых удовлетворяют данной функциональной зависимости, т. е. точек

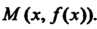Например, графиком функции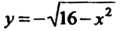Является полуокруж

Ность радиуса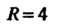С центром в начале координат, расположенная ниже оси

К традиционным основным способам задания функции относятся: аналитический (с помощью одной или нескольких формул); графический (с помощью графика); табличный (с помощью таблицы значений).

Функция заданная формулой

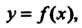(13.1)

Правая часть которой не содержит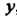, называется явной функцией.

Функция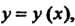Определяемая уравнением

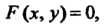(13.2)

Называется функцией, заданной неявно, или неявной функцией.

Отметим, что одно уравнение вида (13.2) может определять несколько функций. Например, уравнение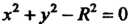Определяет две функции

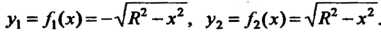
Обратимся к функции (13.1). Каждому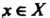По определенному закону ста

Вится в соответствие единственное значение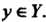С другой стороны, каждому

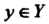Соответствует одно или несколько значений 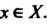В случае, когда каждому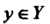По некоторому закону <р соответствует только

Одно значение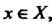Получаем функцию

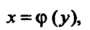(13.3)

Заданную на множестве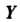Со значениями в множестве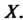Функцию (13.3) называют обратной функцией по отношению к функции (13.1). Функции (13.1) и (13.3) в этом случае называются взаимно обратными. Для взаимно обратных функций выполняются тождества:

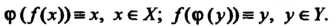
Примеры взаимно обратных функций: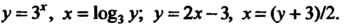

Если придерживаться стандартных обозначений (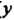- функция,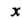-аргумент), то обратную функцию (13.3) следует писать в ввде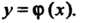Напри

Мер, можно говорить, что функции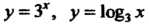Взаимно обратные.

Функцию, обратную к функции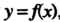, удобно обозначать символом 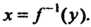Если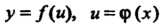- функции своих аргументов, причем область опре

Деления функции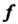Содержит область значений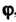, то каждому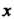Из области определения функции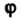Соответствует у такое, что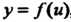, где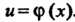. Эта функция, определяемая соответствием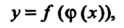

Называется функцией от функции или сложной функцией. (Применяются также и другие названия: композиция функци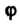йИ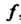, суперпозиция функци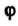йИ)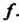

Например, если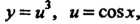То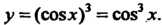

Рассматривают также функции, являющиеся композициями более чем двух функций. Так, функция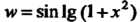Представляет собой композицию сле

Дующих функций: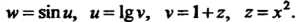

Функция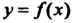Называется четной, если для любых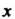И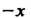Из области ее

Определения выполняется равенство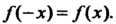Функция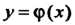Называется

Нечетной, если для любых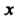И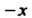Из области ее определения выполняется равенство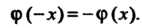Например,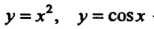- четные функции,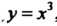, 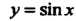- нечетные функции.

Функция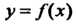Называется периодической, если существует число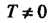

Такое, что при всех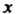И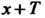Из области ее определения выполняется равенство

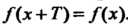. Число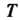В этом случае называется периодом функции. Всякая периодическая функция имеет бесконечное множество периодов. Говоря о периоде функции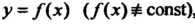, обычно имеют в виду наименьший положительный период: так, периодом функции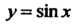Является число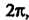Периодом функции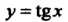— число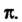

Функция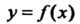Называется ограниченной на множестве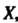, если существует

Такое число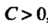, что для всех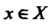Выполняется неравенство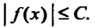

Тригонометрические и обратные тригонометрические функции, функции

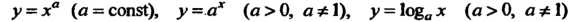Называются

Основными элементарными функциями.

Элементарными функциями называются все функции, которые можно получить из основных элементарных функций с помощью алгебраических действий и образования сложных функций. Например, функции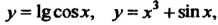 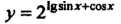И т. д. являются элементарными.

Термин «функция» впервые появился в 1673 г. в одной из работ Лейбница. Под функциями Лейбниц понимал некоторые отрезки прямых. И. Бернулли дал определение функции как аналитического выражения, состоящего из переменной и постоянных величин (1718), он же применил обозначение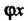(без скобок). Обозначение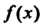Впервые предложил Эйлер в 1734 г.

< Предыдущая		Следующая >