12.12. Представления групп
С точки зрения алгебры изоморфные группы не считаются различными, группе, изоморфной некоторой подгруппе группы подстановок, говорят, что она представлена подстановками.
группе, изоморфной некоторой подгруппе группы подстановок, говорят, что она представлена подстановками.
Теорема 12.5. (Кэли). Каждая конечная группа изоморфна. некоторой группе подстановок (т. е. всякую конечную группу можно представить подстановками).
Следовательно, при описании любой конечной группы можно воспользоваться преимуществами группы подстановок.
Для теории и приложений наиболее интересны линейные представления конечных групп. Говоря о линейном представлении конечной группы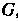 предполагают, что дано векторное пространство
предполагают, что дано векторное пространство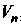 , в котором действуют линейные невырожденные преобразования. Эти преобразования образуют группу
, в котором действуют линейные невырожденные преобразования. Эти преобразования образуют группу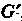 , которой гомоморфна исходная группа
, которой гомоморфна исходная группа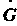 ; при этом говорят, что группа
; при этом говорят, что группа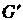 Представляет группу
Представляет группу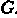
Гомоморфное отображение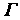 Группы
Группы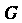 В группу
В группу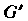 Невырожденных линейных преобразований
Невырожденных линейных преобразований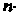 -мерного векторного пространства
-мерного векторного пространства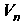 Называется линейным представлением группы
Называется линейным представлением группы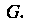
Следовательно, если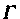 - линейное представление группы
- линейное представление группы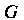 Группой
Группой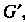 , то каждому элементу
, то каждому элементу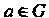 Поставлено в соответствие невырожденное линейное
Поставлено в соответствие невырожденное линейное
Преобразование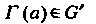 Пространства
Пространства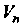 Так, что для любых
Так, что для любых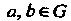 Спра
Спра
Ведливо соотношение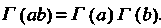 . Как известно, при этом
. Как известно, при этом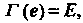 Где
Где
Е,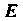 - нейтральные элементы групп
- нейтральные элементы групп Соответственно, и
Соответственно, и
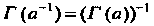 Для любого
Для любого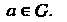
Пространство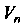 , в котором действуют преобразования из группы
, в котором действуют преобразования из группы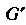 , называется пространством представления группы
, называется пространством представления группы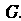 . Размерность пространства
. Размерность пространства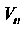 называют размерностью (или степенью) рассматриваемого представления.
называют размерностью (или степенью) рассматриваемого представления.
Вместо линейных преобразований часто рассматривают соответствующие им матрицы.
Ill
Глава 13
| < Предыдущая | Следующая > |
|---|