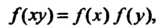12.11. Гомоморфизм групп

Если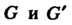— группы и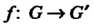— такое отображение, при котором для

Любых элементов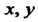Группы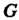

(12.6)

То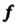Называется гомоморфным отображением или гомоморфизмом группы 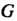в группу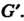Отметим, что в определении гомоморфизма имеется в виду, что каждый элемент группы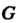Поставлен в соответствие хотя бы одному элементу группы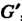, но разным элементам из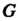Может соответствовать один и тот же элемент из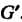. Другими словами, отображение группы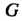В группу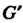Не предполагается взаимно однозначным, как в случае изоморфизма.

Очевидно, каждая группа гомоморфна себе самой, так как можно положить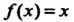Для всех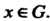Далее, каждая группа гомоморфна единичной группе ( состоящей из одного нейтрального элемента е). Примером гомоморфного отображения групп может служить циклическая группа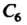Шестого

Порядка с элементами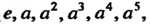Которая гомоморфна циклической

Группе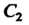Второго порядка с элементами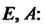

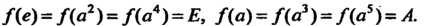
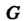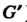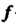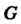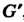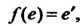Равенство (12.6) означает, что образ произведения двух элементов равен произведению образов этих элементов (которые, впрочем, могут называться по-разному в группахИ), поэтому говорят, что гомоморфизм «сохраняет групповую операцию». Гомоморфизм групп сохраняет не только групповую операцию, но также нейтральный и обратный элементы: если- гомоморфное отображение группыВ группу, тоГде

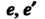— нейтральные элементы групп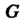И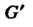Соответственно.

Теорема 12.4. Каждая группа гомоморфна любой своей фактор-группе. Обратно, если группа G гомоморфна группе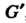, то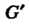Изоморфна факторгруппе G по некоторому нормальному делителю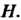

< Предыдущая		Следующая >