12.10. Фактор-группа
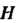
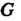
Фактор-группой группы С по нормальному делителю Я называется группа всех смежных классов этой группы С по подгруппе Я.
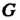
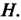
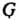
Таким образом, с группой О можно связать некоторый набор новых групп - ее фактор-групп по различным нормальным делителям.
Отметим, что фактор-группа абелевой группы является абелевой; факторгруппа циклической группы — циклической группой.
Примеры фактор-групп.
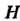
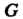
1. Пусть С - аддитивная группа целых чисел, Я - подгруппа чисел, делящихся на 3. Найдем фактор группу С/Я. Групповой операцией в данном случае является сложение. Число смежных классов равно трем (см. пример в п. 12.7): множество чисел, делящихся на 3, два множества чисел, дающих при делении на 3 соответственно остатки 1 и 2. Обозначим эти смежные классы [0], [1], [2]. В этом множестве введем операцию сложения следующим образом: сложив соответствующие числа в квадратных скобках, определим, какой остаток при делении на 3 дает их сумма, и будем считать суммой смежных классов тот, которому принадлежит полученный остаток. Таблица умножения для фактор-группы имеет вид [0]+[0] = [1]+[2] = [2]+[1] = [0], [0]+[1] = [1]+[0] = [2]+[2] = [1], [0]+[2] = [2]+[0] = [1]+[1 ]= [2]. Отсюда видно, что фактор-группа абелева. Кроме того, все смежные классы порождаются классом [1], они совпадают со степенями этого класса: [1], Р]+П]=[2], [1]+[1]+[1] = [0]. Поскольку фактор-группа порождена одним элементом, то она циклическая.
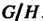
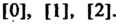
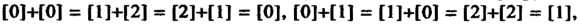
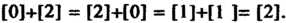
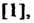
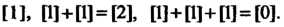
2. Пусть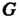
— аддитивная группа целых чисел,
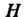— подгруппа целых чисел, кратных натуральному числу
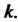Фактор-группой
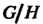Является конечная
Группа порядка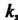
Состоящая из классов
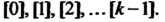Эта фактор
Группа циклическая, как и сама группа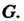
3. Пусть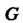
- мультипликативная группа всех невырожденных матриц порядка
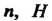- подгруппа матриц с определителем, равным единице. Фактор-группа
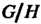Изоморфна мультипликативной группе отличных от нуля действительных чисел.
| < Предыдущая | Следующая > |
|---|
