12.09. Классы сопряженных элементов
Элементы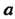 И
И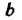 Группы
Группы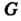 Называют сопряженными, если в
Называют сопряженными, если в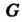 Существует хотя бы один такой элемент д:, что
Существует хотя бы один такой элемент д:, что
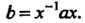 (12.5)
(12.5)
В этом случае говорят, что элемент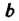 Получается из элемента а трансформирова-
Получается из элемента а трансформирова-
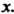
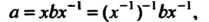
А=хЬх~1 =(х~1)~'Ьх~\
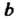
Т. е. элемент а при этом получается из элемента Ъ трансформированием элементом х~1..
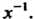
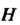
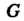
Теорема 12.2. Подгруппа Н группы С тогда и только тогда будет нормальным делителем в С, если вместе с любым своим элементом И она содержит все элементы, сопряженные с ним в С.
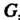
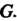
Замечание. Нормальный делитель называют также инвариантной подгруппой. Из теоремы 12.2 следует происхождение этого названия. Если Н - нормальный делитель группы С, то трансформирование любого элемента подгруппы Н с помощью элемента группы С дает снова элемент подгруппы Н (подгруппа Н остается неизменяемой по отношению к операции трансформирования элементов Н ).
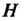
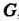
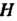
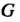
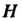
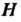
Теорема 12.3. Пересечение двух нормальных делителей группы является нормальным делителем этой группы.
| < Предыдущая | Следующая > |
|---|