12.08. Нормальный делитель

Подгруппа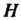Группы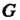Называется нормальным делителем этой группы (или инвариантной подгруппой), если левостороннее и правостороннее разложения этой группы по указанной подгруппе совпадают.

Из определения следует, что любая подгруппа коммутативной группы является в ней нормальным делителем. Далее, в любой группе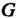Сама группа и ее единичная подгруппа будут нормальными делителями: разложение группы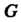По самой этой группе состоит из одного элемента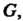Разложения группы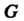По единичной подгруппе совпадают с разложением группы на отдельные элементы. Приведем примеры нормальных делителей в некоммутативных группах.

1.  В симметричной группе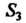(см. п. 12.4) подгруппа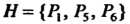Является нормальным делителем, так как левостороннее и правостороннее разложения совпадают, они состоят из двух классов: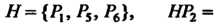

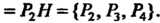
2.  В мультипликативной группе невырожденных квадратных матриц порядка и подгруппа матриц с определителем, равным единице, будет нормальным делителем. Действительно, левый и правый смежные классы по этой подгруппе, порождаемые матрицей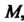, совпадают с классом всех матриц, определитель которых равен определителю матрицы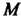(как известно, определитель произведения двух матриц равен произведению определителей этих матриц).

Можно дать и другие определения нормального делителя, равносильные исходному. Приведем одно из них.

Подгруппа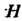Группы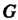Называется нормальным делителем этой группы, если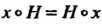Для любогоТ. е. для любого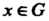И элемента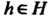Существуют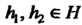Такие, что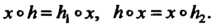

< Предыдущая		Следующая >