12.05. Группа вращений правильного многоугольника. Циклические группы. Группа симметрий правильного треугольника

 

Пусть дан правильный и-угольник Л, А2 ... А„ с центром в точке О (рис. 12.1,

И = 6). Рассмотрим всевозможные повороты плоскости вокруг точки О, при которых этот правильный и-угольник совмещается сам с собой. Таких поворотов будет п :а0 - поворот на угол <р0 = 0 (тождественное преобразование); я, - поворот на угол ф, = 2я/л, аг - поворот на угол ф2= = (2я/и)2,...,а„_, - поворот на угол ф„_, =(2я/и)(и-1). Под умножением  ф*  /I А*

Поворотов будем понимать последовательное их выполнение: акоа, = аки, причем ак+п = ак при любом к (к = 0,1, 2,..., и), в частности а„ = а0. Умножение поворотов является ассоциативным (и коммутативным).

Множество указанных поворотов правильного многоугольника образует группу по умножению, роль единицы играет тождественное преобразование - поворот а0. Для каждого элемента ак существует обратный элемент ак1=а„_к (А: = 0,1,2,..., п-1), так как ак °а„^к =ап =<%, т. е. ак °а„_к =а0, где а0 - единичный элемент.

Положим а, = а, тогда а2 =а2,а3 =а3,...,а„_1 =а"~х, ап =а". В этом случае

Говорят, что группа образована степенями одного из своих элементов (или что она порождается одним из своих элементов); таким элементом является элемент а = а,. Группы, образованные степенями одного из своих элементов, называются циклическими. Таким образом, группа вращения правильного и-угольника является циклической группой порядка и, эта группа обозначается С„. Отметим, что аддитивная групйа целых чисел также будет циклической, она

Порождается одним из своих элементов - числом 1: 2 = 1+1, 3 = (1 +1)+1 и т. д. Эта группа является бесконечной циклической группой, ее обозначают С„.

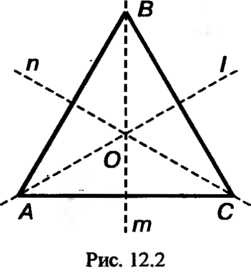
Пусть дан правильный треугольник А ВС с центром в точке О (рис. 12.2). Рассмотрим все симметрии данной фигуры, т. е. те преобразования плоскости, при которых этот треугольник переходит в себя (или самосовмещается). К ним относятся: три поворота ф0, ф,, ф2 плоскости вокруг точки О соответственно на углы

0,2я/3,4я/3 (частный случай рассмотренных выше вращений правильного и-

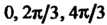
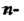
Угольника при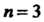); три осевых симметрии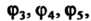Определяемых соот

Ветственно осями симметрии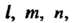Прохо

Дящими через вершину правильного треугольника и середину его противоположной стороны (см. рис. 12.2).

Будем характеризовать каждое самосовмеще-ние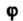Подстановкой на множестве вершин 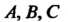Правильного треугольника

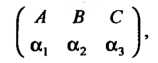
Где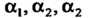- те же буквы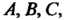Взятые в

Некотором порядке. Принятое нами соответствие между самосовмещениями треугольника и подстановками множества его вершин дает

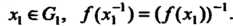
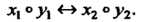
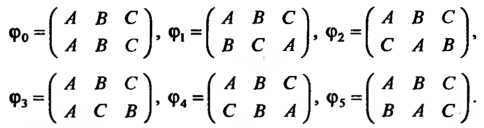
Множество самосовмещений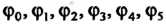Образует группу относитель

Ного умножения (последовательного выполнения двух самосовмещений). Роль единицы играет тождественное преобразование, каждый элемент данного преобразования имеет обратный. Эта группа называется группой симметрий треугольника.

< Предыдущая		Следующая >