12.04. Группы преобразований. Симметрическая группа n-й степени

 

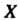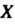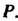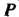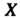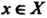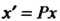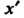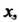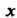Преобразованием множестваНазывается взаимно однозначное отображение этого множества на себя. Преобразование множестваОбозначим буквойОпределение преобразованияМножестваОзначает следующее:любому элементуСтавится в соответствие единственный элемент того же множества;Называется образом элементаА- прообразом 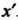Каждый элемент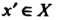Имеет единственный прообраз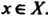

Умножением преобразований называется последовательное их выполнение. Произведение двух преобразований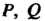Обозначается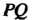(справа записано то преобразование, которое выполняется первым; по определению 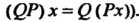Очевидно, произведение двух преобразований данного множества является преобразованием данного множество. Отметим, что в общем случае умножение не является коммутативным, т. е.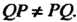Можно показать, что произведение преобразований подчиняется ассоциативному закону. Роль единицы при умножении преобразований выполняет тождественное преобразование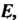Ставящее в соответствие каждому элементу множества его самого. Для каждого преобразования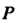Существует обратное преобразование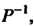Которое каждому элементу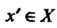Ставит в соответствие его единственный прообраз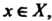Причем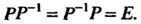Следовательно, множество преобразований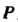Данного множества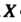Образует группу.

Если множество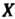Конечно и состоит из п элементов, то всевозможные взаимно однозначные отображения этого множества на себя называются подстановками. Подстановку из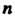Элементов можно обозначить так:

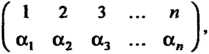
Где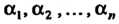- те же числа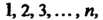Обозначающие данные элементы и

Записанные в другом порядке.

Примеры подстановок при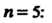

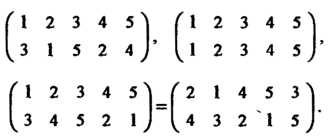
Первая подстановка означает такое взаимно однозначное отображение множества 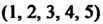На себя, при котором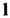Переходит в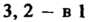И т. д. Вторая подста

Новка называется тождественной, каждый элемент соответствует сам себе. Равенство двух других подстановок показывает, что расположение столбцов в записи подстановки не играет роли. Подстановки, отличающиеся только порядком следования столбцов, не считаются различными.

Умножением подстановок называют последовательное их выполнение (сначала правого сомножителя, затем левого). Умножение подстановок ассоциативно, но не коммутативно. Например, если

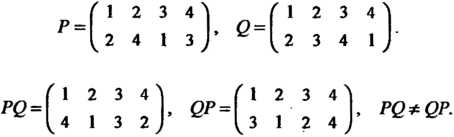
Единицей при умножении подстановок из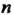Элементов служит тождественная подстановка

Каждая подстановка из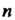Элементов имеет обратную:

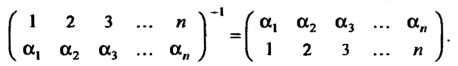
Чтобы получить подстановку, обратную данной, необходимо поменять местами строки.

 

Множество подстановок из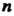Элементов относительно введенной операции умножения образует группу. Группа подстановок из п элементов называется симметрической группой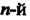Степени и обозначается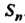. Число подстановок из п элементов равно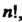Поэтому группа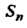Имеет порядок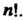

Рассмотрим группу подстановок из трех элементов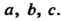Поскольку из трех элемен

Тов можно составить шесть различных перестановок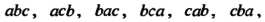То

И число различных подстановок для них равно шести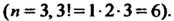 Обозначим эти подстановки следующим образом:

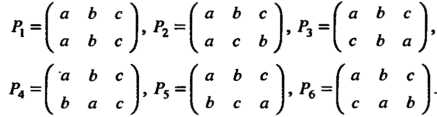
Отметим, что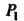- тождественная подстановка; для каждой подстановки существует обратная:

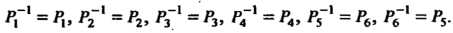
Группа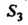(симметрическая группа подстановок из 3 элементов) некоммутативна, поскольку, например,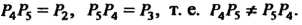

Таблица 12.1

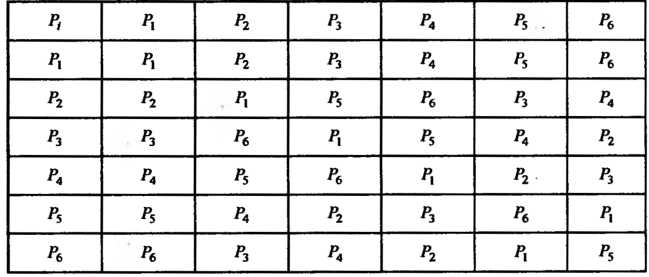
Группу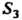Можно представить следующей таблицей умножения, в которой слева стоят левые множители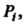Сверху - правые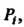А на пересечении соответствующей строки и столбца - их произведение. Таблицы такого рода называют таблицами Кэли (табл. 12.1).

 

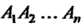
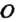
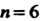
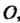
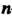
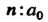
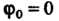
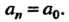
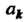
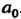
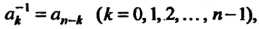
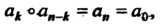
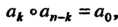
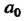
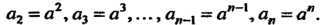
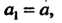
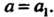
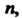
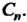
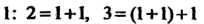
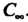
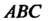
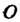
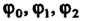
< Предыдущая		Следующая >