12.03. Подгруппа
Подгруппой группу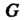
Называется подмножество
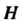Ее элементов, образующее группу относительно операции, определенной в
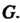Чтобы убедится в том, что множество
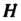Группы
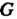Является ее подгруппой, необходимо проверить, что:
1) произведение (сумма) любых двух элементов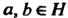
Принадлежит
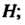2) для
Любого элемента
Обратный элемент принадлежит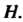
Этого будет достаточ
Но, так как ассоциативный закон выполняется для любых трех элементов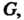
В том числе и для элементов
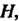А нейтральный элемент
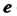(1 или 0) будет принадлежать
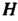(как произведение
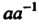Или сумма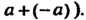
Примеры подгрупп некоторых групп.
I. Множество всех действительных чисел является аддитивной группой.
Подгруппами аддитивной группы всех действительных чисел являются в частности, следующие: 1) аддитивная группа рациональных чисел; 2) аддитивная группа целых чисел; 3) аддитивная группа всех целых чисел, кратных числу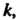
например аддитивная группа четных чисел.
Группа целых чисел является подгруппой группы рациональных чисел.
Замечание 1. Множество нечетных чисел не образует группу по сложению, так как сумма двух нечетных чисел является четным числом (и не принадлежит данному множеству).
П. Мультипликативная группа всех действительных чисел, отличных от нуля, имеет, в частности, следующие подгруппы: !) мультипликативную группу положительных действительных чисел; 2) мультипликативную группу рациональных чисел, отличных от нуля; 3) множество, состоящее из двух чисел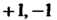
С операцией умножения.
Замечание 2. Мультипликативная группа положительных действительных чисел не является подгруппой аддитивной группы всех действительных чисел, так как групповые операции в рассматриваемых множествах - разные (соответственно умножение, сложение).
Ш. Мультипликативная группа невырожденных матриц порядка п имеет, в частности, подгруппы: 1) группу ортогональных матриц; 2) группу диагональных матриц; 3) группу матриц с положительным определителем; 4) группу матриц с определителем, равным единицы (эта группа называется унимодулярной).
Пересечение двух подгрупп группы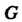
Является подгруппой в
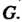Например, в аддитивной группе целых чисел пересечение подгруппы четных чисел и подгруппы чисел, кратных трем, будет подгруппой чисел, кратных шести.
Каждая группа является своей подгруппой. Далее, каждая группа имеет единичную подгруппу, состоящую из одного нейтрального элемента (единицы или нуля). Эти две подгруппы называются несобственными (или тривиальными) подгруппами. Остальные подгруппы называются собственными (или истинными) подгруппами. В любой группе все подгруппы каждой группы являются в тоже время подгруппами исходной группы. Например, аддитивная группа целых чисел является подгруппой аддитивной группы рациональных чисел, которая в свою очередь есть подгруппа аддитивной группы всех действительных чисел; аддитивная группа целых чисел — подгруппа аддитивной группы всех действительных чисел.
| < Предыдущая | Следующая > |
|---|
