12.02. Примеры групп
1. Множество всех целых чисел с операцией сложения образует аддитивную группу. Действительно, сумма а+Ь двух целых чисел а и Ь также является целым числом. В этом случае говорят, что множество целых чисел замкнуто относительно операции сложения. Сложение целых чисел коммутативно: (а+Ъ) + с = а+(Ъ+с). В данном множестве имеется нейтральный элемент, т. е. число 0 такое, что а + 0 = а при любом целом числе а. Для каждого элемента целого числа о существует обратный элемент (противоположное число), т. е. такое число - а, что а + (-а) = 0. Рассматриваемая группа является коммутативной, так как а + Ь = Ь+а.
Замечание 1. Множество всех целых чисел не образуют группу по умножению, так как обратные для целых чисел (отличных от -1 и 1) не являются
Целыми числами. Например, для числа 2 обратное число 2~' не принадлежит множеству целых чисел.
2. Множество всех действительных чисел, отличных от нуля, с операцией умножения образует мультипликативную группу. Эта группа является коммутативной, так как аЬ = Ьа.
Замечание 2. Множество всех действительных чисел не образует группу по умножению, поскольку для числа 0 нет обратного.
3. Множество всех векторов трехмерного пространства образует группу по сложению. Эта группа является коммутативной (а + Ь= Ь+а).
4. Множество матриц размером тхп образует коммутативную группу по сложению (А + В= В + А). Для матрицы А обратным элементом является матрица (- А); нейтральный элемент - нулевая матрица О.
5. Множество всех невырожденных квадратных матриц порядка п образует мультипликативную группу. Эта группа, которую называют полной линейной группой, не является коммутативной ( в общем случае АВ * ВА).
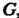
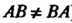
Замечание 3. Множество всех квадратных матриц порядкап не образует группу по умножению, так как для некоторых его элементов нет обратных (вырожденная матрица не имеет обратной).
6. Множество всех невырожденных линейных преобразований линейного пространства образует мультипликативную группу.
7. Множество, состоящее из двух чисел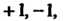 Образует группу по умножению. Действительно, каждой из произведений
Образует группу по умножению. Действительно, каждой из произведений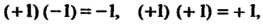
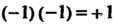 Принадлежит данному множеству. Умножение ассоциативно. Существует единица - число
Принадлежит данному множеству. Умножение ассоциативно. Существует единица - число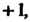 Которое удовлетворяет условию
Которое удовлетворяет условию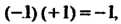
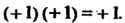 Для каждого элемента существует обратный: каждое из этих двух чисел совпадает со своим обратным.
Для каждого элемента существует обратный: каждое из этих двух чисел совпадает со своим обратным.
Замечание 4. Множество, состоящее из двух чисел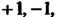 Не образу
Не образу
Ет группу по сложению, так как сумма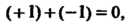 А число
А число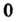 Не принадлежит
Не принадлежит
Данному множеству. (В таком случае говорят, что данное множество не является замкнутым относительно операции сложения).
8. Множество, состоящее из одного элемента 0, образует аддитивную группу. Действительно,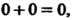 Сумма принадлежит данному множеству. Свойства операции сложения очевидны.
Сумма принадлежит данному множеству. Свойства операции сложения очевидны.
9. Множество, состоящее из одного элемента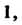 Образует мультипликативную группу.
Образует мультипликативную группу.
Группа, образованная одним элементом, называется единичной.
| < Предыдущая | Следующая > |
|---|