12.01. Понятие группы. Основные определения

 

Группой называется множество С элементов а, Ъ, с,..., для которых определена операция (сложения или умножения), которая каждой упорядоченной паре (а, Ь) элементов С ставит в соответствие единственный элемент с = а о Ъ данного множества, причем операция обладает следующими свойствами:

1)  операция ассоциативна, т. е. для любых а, Ь, сеС

А°(Ь°с) = (а°Ь)°с;  (12-1)

2)  в С существует нейтральный элемент е такой, что для любого элемента а е С

А°е = е°а = а;  (12.2)

3)  для каждого элемента а е С существует обратный ему элемент а-1 такой, что

А о а-1 =е, а~1 оа = е.  (12.3)

Если, кроме того, для любых а, Ь е О выполняется условие

А°Ь=Ьоа,  (12-4)

То группа называется коммутативной или абелевой группой.

В любой группе нейтральный элемент определен однозначно; для каждого элемента существует единственный обратный элемент.

Группа состоящая из конечного числа элементов, называется конечной. Число элементов группы называют ее порядком. Группа, не являющаяся конечной, называется бесконечной.

Группа называется аддитивной или группой по сложению, когда групповая операция, ставящая в соответствие паре элементов (а, Ь) элемент с = а°Ъ, является сложением. В этом случае символ операции ° заменяется знаком +; с = а + Ь, нейтральный элемент называют нулем и обозначают символом 0;

А + 0 = 0+а = а. Элемент, обратный к элементу а, называют противоположным и обозначают - а:а +(-о) = (-о) +а = 0.

Группа называется мультипликативной или группой по умножению, когда групповая операция, ставящая в соответствие упорядоченной паре (а, Ь) элемент с = а°Ь, является умножением. В данном случае произведение а°Ъ обозначается а ¦ Ь или аЬ; нейтральный элемент называется единицей и обозначается символом 1: а-1 = 1- д = о.

Произведение и элементов, равных а, называют п-й степенью элемента а и обозначают а". Отрицательные степени элемента а можно определить или как эле-

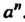
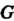
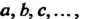
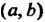
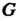
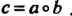
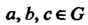
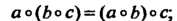
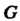
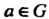
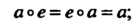
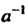
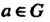
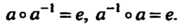
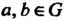
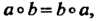
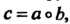
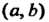
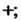
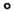
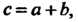
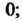
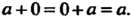
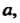
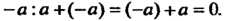
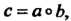
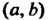
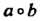
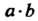
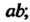
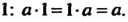
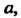
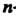
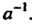
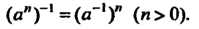
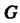
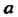
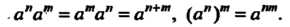
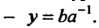
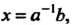
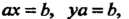
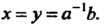
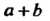
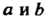
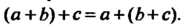
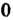
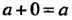
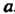
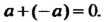
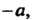
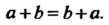
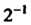
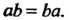
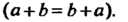
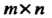
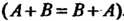
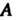
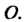
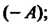
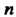
Менты группы С, обратные положительным степеням, или как произведения соответствующего числа множителей, равных элементу в-1. Эти определения совпадают, так как верно равенство

(«"Г1 =(«-')" (и> 0).

В любой группе С для степеней каждого элемента а при любых показателях т и п (положительных, отрицательных или нулевых) выполняются равенства

„п„т „т „п_ „п+т /„п\т_ „пт

I  а а = а а = а, (а ) =а.

Если операция в группе называется сложением, то вместо степеней элемента а говорят о кратных этого элемента и пишут па.

В каждой мультипликативной группе однозначно разрешимы уравнения ах = Ь, у а = Ь, первое из них имеет решение х = а~'Ь, второе - у = Ъа~\

Если группа является коммутативной, то эти уравнения не различаются, они имеют одинаковые решения х = у = а~'Ь.

 

< Предыдущая		Следующая >