11.8. Упрощение уравнений фигур второго порядка в пространстве
Фигурой второго порядка в пространстве называется множество точек пространства, декартовы координаты которых удовлетворяют уравнению
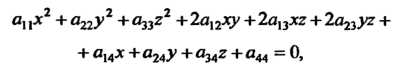(11.32)
Где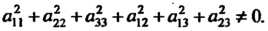
Сумма первых-шести членов левой части уравнения (11.32) представляет собой квадратичную форму трех переменных,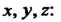
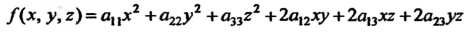(11.33)
С симметрической матрицей
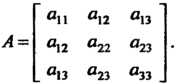(11.34)
Фигура второго порядка называется центральной, если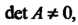
И нецен
Тральной, если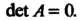
С помощью ортогонального преобразования квадратичную форму (11.33) можно привести к каноническому виду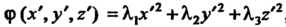
, где 
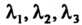- корни характеристического уравнения
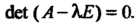Матрица
Квадратичной формы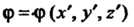
Принимает вид
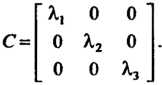(11.35)
Указанное ортогональное преобразование приводит уравнение (11.32) к виду
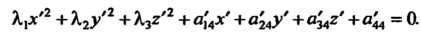(11.36)
Центральные фигуры. Если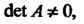
То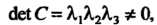
Так как
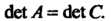Выделяя полные квадраты в левой части уравнения (11.36), можно привести его к виду
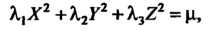
(11.37)
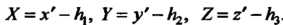
Поскольку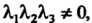
То ни одно из чисел не равно нулю, все эти числа могут
Иметь один знак _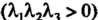
_ или только два из них одного знака.
1. Если все числа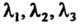
Одного знака, то уравнение (11.37) можно привести к одному из следующих канонических видов:
(11.38)
(11.39)
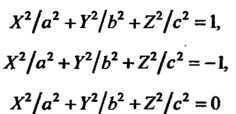(11.40)
В зависимости от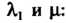
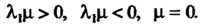
Уравнение (11.38) определяет эллипсоид, уравнению (11.39) не удовлетворяют координаты ни одной точки пространства, уравнению (11.40) удовлетворяют координаты единственной точки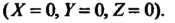
2. Пусть знак одного из этих чисел противоположен знаку двух других: предположим, что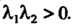
Уравнение (11.37) можно привести к одному из канонических видов
(11.41)
(11.42)
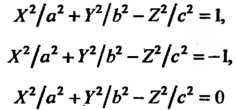(11.43)
В зависимости от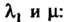
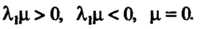
Уравнения (11.41) — (11.43) определяют соответственно однополосный гиперболоид, двуполостный гиперболоид и конус второго порядка.
Нецентральные фигуры. Ес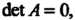ли
Или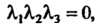
То одно или два из
Этих чисел равны нулю.
1. Пусть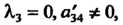
Тогда уравнение (11.36) приводится к виду
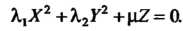(11.44)
Если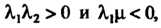
То имеем
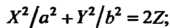(11.45)
В случае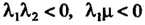
Получаем
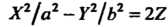(11.46)
Уравнения (11.45) и (11.46) определяют соответственно эллиптический и гиперболический параболоиды.
2. Пусть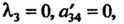
Тогда имеем уравнение
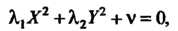(11.47)
Которое приводится к одному из следующих канонических видов:
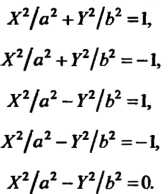
(11.48)
(11.49)
(11.50)
(11.51)
(11.52)
Уравнение (11.48) определяет эллиптический цилиндр, каждое из уравнений (11.51), (11.50) — гиперболический цилиндр, уравнение (11.52) - пару пересекающихся плоскостей; уравнению (11.49) не удовлетворяют координаты ни одной точки.
3. Есл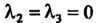и
И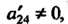
То уравнейие (11.36) приводится к виду
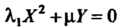Или
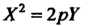(11.53)
И определяет параболический цилиндр.
4. Есл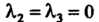и
И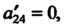
То имеем уравнение
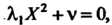Которое приводится к одному из канонических видов
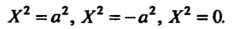(11.54)
Первое из уравнений (11.54) определяет пару параллельных плоскостей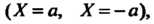 
Третье, уравнение — пару совпавших плоскостей; второму уравнению не удовлетворяют координаты ни одной точки пространства.
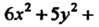
Пример 11.5. Какую поверхность определяет уравнение 6х2 + 5у2 + + 7г2 - 4ху + 4хг = 18?
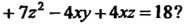
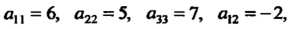
Это уравнение вида (11.32), для которого аи = 6, о22 = 5, а33 = 7, а12 = -2,
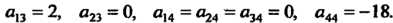
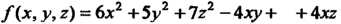
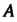
О, з = 2, а23 = 0, а,4 = а24 = а34 = 0, а44 = -18. Левая часть данного уравнения является квадратичной формой /(х, у,г) = 6х2 +Ъу2 +7г2 -4ху + +4хг трех переменных х, у, г (х = х],у = х2,г = х3). Составим матрицу А этой квадратичной формы и характеристическое уравнение матрицы А:
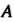
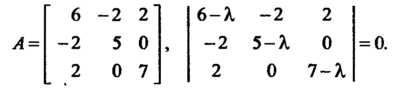
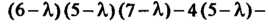
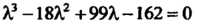
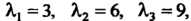
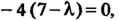
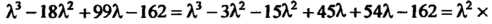
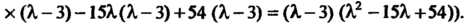
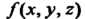
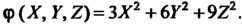
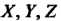
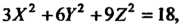
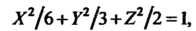
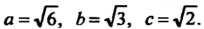
Характеристическое уравнение (6-Я) (5-Я) (7-Я)-4(5-Я)-
-4(7-Я)=0, или Я3-18Я2+99Я-162 = 0 имеет корни Я,=3, Я2=6, Я3=9, (так как Я3-18Я2 +99Я-162 = Я3-ЗЯ2-15Я2 +45Я.+54Я-162 = Я2 х
Х (Я - 3) - 15Я(Я - 3) +54 (Я - 3) = (Я - 3) (Я,2 - 15Я +54)).
Следовательно, квадратичную форму /(х, у,г) можно привести к виду <р(Х, У,2) = ЗХ2+6У2+922. В новых координатах Х, У,2 данное уравнение имеет вид ЗА*2 +6У2 +922 = 18, или
Х2/б + у2/з + 21/2 = 1, оно определяет эллипсоид с полуосями о=л/6, Ь = Л, с = Л-
Гпава 12
ГРУППЫ
| < Предыдущая | Следующая > |
|---|
