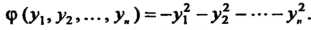11.5. Знакоопределенные квадратичные формы
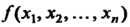
Действительная квадратичная форма /(х,, х2, называется положитель
Но-определенной, если она приводится к нормальному виду, состоящему из л положительных квадратов: /(х],х2,...,х„)~у(у1,у2,...,у„), где
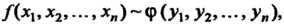
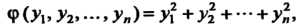
Ч>(.У1,У2,-,У„) = У?+у1+-+У*, (Н.9)
Т. е. если ранг и положительный индекс инерции равны числу неизвестных.
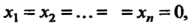
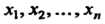
Систему значений хих2,...,хП назовем нулевой, если хх=х2=...= = х„ = О, и ненулевой, если хотя бы одно из них отлично от нуля.
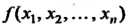
Т ео рем а 11.6. Действительная квадратичная форма /(*,, *2,..., х„) является положительно-определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных
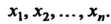
*1> Х2у... , Хп.
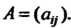
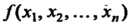
Пусть дана квадратичная форма /(хи х2,... ,хп) с матрицей А = (ац). Главными минорами квадратичной формы/называются миноры
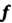
Т. е. миноры порядка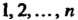
Матрицы
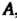, расположенные в левом верхнем углу;
Последний из них совпадает с определителем матрицы.
Теорема 11.7. Квадратичная форма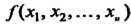
С действительной
Матрицей является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны.
Действительная квадратичная форма называется отрицательно-определенной, если она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных; эту форму можно привести к виду
Теорема 11.8. Квадратичная форма является отрицательно-определенной тогда и только тогда, когда ее главные миноры четного порядка положительны, а нечетного — отрицательны.
Положительно-определенные и отрицательно-определенные квадратичные формы называются знакоопределенными квадратичными формами.
Вырожденные квадратичные формы, нормальный ввд которых состоит из квадратов одного знака, называются полуопределенными.
Неопределенными называются квадратичные формы, нормальный вид которых содержит как положительные, так и отрицательные квадраты переменных.
Пример 11.2. Доказать, что квадратичная форма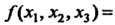
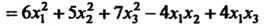Положительно-определенная.
Запишем матрицу А этой квадратичной формы и определитель матрицы А:
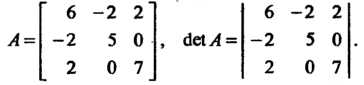
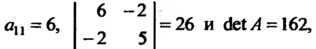
Т. е.
Так как главные миноры матрицы
Все положительны, то данная квадратичная форма является положительно-определенной.
| < Предыдущая | Следующая > |
|---|
