11.3. Приведение действительной квадратичной формы к нормальному виду

Квадратичная форма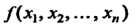Называется канонической, если она не

Содержит произведений различных переменных, т. е.

(И-8)

Каноническая квадратная форма называется нормальной (или имеет нормальный ввд), если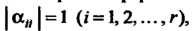Т. е. отличные от нуля коэффициенты при

Квадратах переменных равны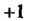Или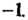Например, квадратичная форма

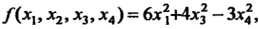Для которой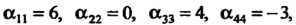

Имеет канонический вид; квадратная форма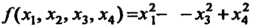Явля

Ется нормальной, так как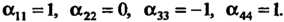

Теорема 11.2. Любая квадратичная форма некоторым невырожденным линейным преобразованием может быть приведена к каноническому виду

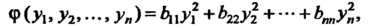
Где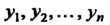- новые переменные.

Некоторые из коэффициентов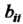Могут оказаться равными нулю; число отличных от нуля коэффициентов в этой формуле равно рангу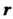Матрицы квадратичной формы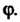

Теорема 11.3. Любую действительную квадратичную форму линейным невырожденным преобразованием можно привести к нормальному виду

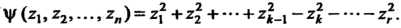
V(г„22,..., гл) = г* +х\  -г\-----г2.

Число входящих сюда квадратов равно рангу формы.

< Предыдущая		Следующая >