11.2. Преобразование квадратичной формы при линейном однородном преобразовании переменных

Рассмотрим квадратичную форму (11.1). Перейдем к новым переменным 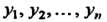По формулам

Или в матричном виде где

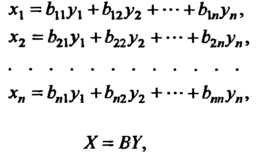
(11.5)

(11.6)

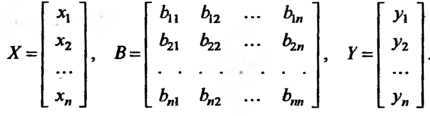
В квадратичной форме (11.1) вместо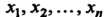Подставим их выражения

I через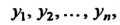Определяемые формулами (11.5), получим квадратичную

(11.7)

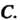
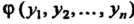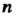ФормуIПеременных с некоторой матрицей В этом случае го

Ворят, что квадратичная форма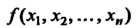Переводится в квадратичную форму

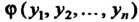Линейным однородным преобразованием (11.5). Линейное однородное преобразование (11.6) называется невырожденным, если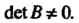

Две квадратичные формы называются конгруэнтными, если существует невырожденное линейное однородное преобразование, переводящее одну форму в другую. Есл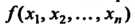иИ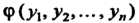Конгруэнтны, то будем писать

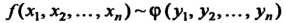
Свойства конгруэнтности квадратичных форм.

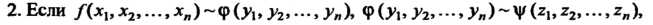
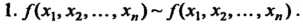
То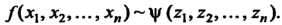

Теорема 11.1. Квадратичная форма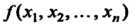С матриц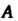ейЛиней

Ным однородным преобразованием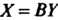Переводится в квадратичную форму

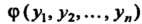С матрицей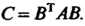

Следствие 1. Определители матриц конгруэнтных невырожденных действительных квадратичных форм имеют одинаковые знаки.

Следствие 2. Конгруэнтные квадратичные формы имеют одинакосые ранги.

< Предыдущая		Следующая >