11.1. Квадратичная форма и ее матрица

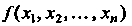
Квадратичной формой /(хих2,...,х„) п действительных переменных х1,х2,...,х„ называется сумма вида

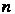
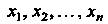
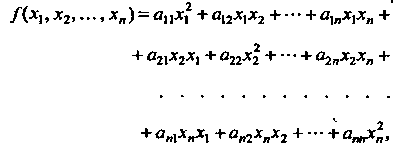
Или

Д*1» *2. . *„) = ^ ^аих1х]’  О,2)

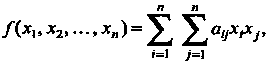
.=1 7=1

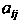
Где о, у - некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что о, у = а;,.

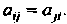
Квадратичная форма называется действительной или комплексной в зависимости от того, являются ли ее коэффициенты соответственно действительными или комплексными числами. Будем рассматривать действительные квадратичные формы.

Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (11.1) соответствует единственная симметрическая матрица

(11.3)

И наоборот, всякой симметрической матрице (11.3) соответствует единственная квадратичная форма с точностью до обозначения переменных.

Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма п переменных называется невырожденной, если ее матрица невырожденная, т. е. г = п, и вырожденной, если г < п.

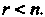
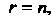
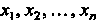
Квадратичную форму (11.1) п переменных хх, х2, ...,х„ можно записать в матричном вцце. Действительно, если X - матрица-столбец из переменных

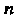
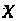
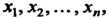
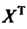- матрица, полученная транспонированием матрицы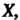Т. е. матрица-строка из тех же переменных, то

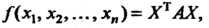(11.4)

Где А определяется формулой (11.3).

Пример 11.1. Записать матрицу квадратичной формы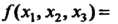

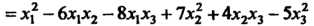И найти ее ранг.

В данном случае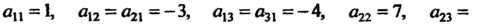

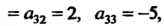Поэтому

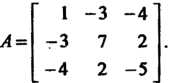
Вычислим определитель этой матрицы

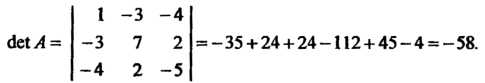
Так как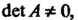То ранг матрицы равен трем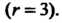Эта квадратичная форма

Является невырожденной, поскольку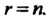

< Предыдущая		Следующая >