10.10. Ортогональные преобразования
Линейное преобразование евклидова пространства называется ортогональным, если в некотором ортонормированием базисе его матрица ортогональна.
Теорема 10.14. Линейное преобразование евклидова пространства является ортогональным тогда и только тогда, когда оно ортонормированный базис переводит в ортонормированный.
Теорема 10.15. Ортогональное преобразование не меняет скалярного произведения векторов.
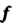
Следствие 1. При ортогональном преобразовании / остается неизменной норма вектора, т. е. | х || = | Дх) |
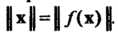
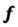
Следствие 2. При ортогональном преобразовании / остается неизменным угол между векторами, т. е.
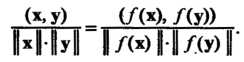
(*> У) (/(х), /(у))
Ортогональные преобразования обладают следующими свойствами.
1. Ортогональное преобразование является невырожденным.
2. Для любого ортогонального преобразования существует обратное преобразование, являющееся ортогональным.
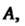
3. Если ортогональное преобразование имеет матрицу А, то обратное ему преобразование имеет матрицу АТ.
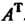
4. Произведение двух ортогональных преобразований является ортогональным преобразованием.
| < Предыдущая | Следующая > |
|---|