10.09. Ортогональные матрицы
Матрица
Называется ортогональной, если соответствующая ей система векторов
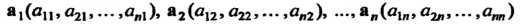(10.19)
Является ортонормированной.
Векторы (10.19) будут ортонормированными (см. п. 9.7), если
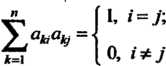
Для любых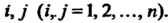
Примеры ортогональных матриц:
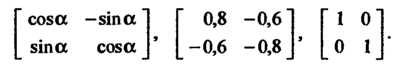
Отметим, что единичная матрица любого порядка является ортогональной.
Теорема 10.12. Необходимое и достаточное условие ортогональности матрицы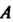
Выражается равенством
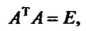
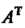
Где - матрица, полученная из матрицы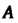
Транспонированием,
-
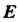Единичная матрица того же порядка, что и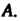
Следствие 1. Модуль определителя ортогональной матрицы равен единице.
Следствие 2. Ортогональная матрица является невырожденной матрицей.
Следствие 3. Произведение двух ортогональных матриц есть ортогональная матрица.
Следствие 4. Равенство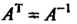
Выражает необходимое и доста
Точное условие ортогональности матрицы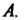
Следствие 5. Матрица, полученная транспонированием ортогональной матрицы, является ортогональной.
Следствие 6. Матрица, обратная ортогональной матрице, является ортогонал ьной.
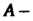
Замечания. 1. Из условия де1А = ± 1 не следует, что А-
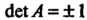
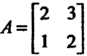
Г2 3]
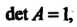
Ортогональная матрица. Например, матрица Л = I I, для которой Йе1 А = 1, не
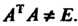
Является ортогональной, так как АтА Ф Е.
2. Сумма ортогональных матриц не является ортогональной матрицей.
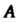
3. Необходимое и достаточное условие ортогональности матрицы А можно выразить равенством АА = Е.
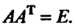
Теорема 10.13. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.
| < Предыдущая | Следующая > |
|---|
