10.08. Невырожденные линейные преобразования. Преобразование, обратное данному
Линейное преобразование называется невырожденным, если его матрица является невырожденной; в противном случае линейное преобразование называется вырожденным.
Теорема 10.10. Линейное преобразование является невырожденным тогда и только тогда, когда оно взаимно однозначно.
Следствие. Линейное невырожденное преобразование ненулевой вектор переводит в ненулевой; обратно также верно: если линейное преобразование ненулевой вектор переводит в ненулевой, то оно будет невырожденным.
Теорема 10.11. Произведение двух линейных невырожденных преобразований есть невырожденное линейное преобразование. Преобразование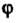
Называется обратным преобразованию
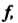Если для любого вектора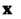
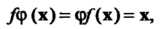(10.17)
Т. е. произведение этих преобразований является тождественным преобразованием. Из определения следует, что если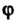
— преобразование, обратное преобразованию
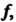То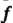
- преобразование, обратное
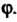Преобразования
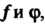Удовлетворяющие условию (10.17), называются взаимно обратными.
Линейное преобразование имеет обратное преобразование тогда и только тогда, когда оно является невырожденным.
Для любого невырожденного линейного преобразования с матрицей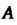
В некотором базисе существует единственное обратное преобразование с матрицей
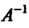в том же базисе.
Пр и м е р 10.6. Найти линейное преобразование, обратное преобразованию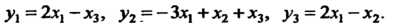
Это преобразование имеет матрицу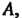
Определитель которой отличен от нуля, поэтому для него существует обратное преобразование с матрицей
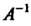. Так как
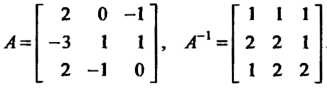
То обратное преобразование выражается формулами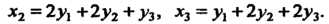 
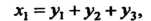
(10.18)
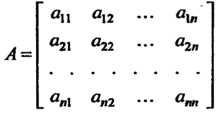
| < Предыдущая | Следующая > |
|---|
