10.07. Действия над линейными преобразованиями

 

Произведение преобразований. Рассмотрим преобразование/, переводящие вектор х в вектор у, т. е. у = Дх). К вектору у применим преобразование переводящие вектор у в вектор г, т. е. г= #(у). Так как у = Дх), то имеем преобразование 2=&(/(х)), переводящее вектор х в вектор г, причем г получен в результате последовательного применения преобразований / и #. Преобразование, заключающееся б последовательном применении преобразований / и называется произведением - преобразования / на преобразование # или композицией этих преобразований и обозначается % ° / (или просто ); отметим, что справа записывается первое преобразование. Таким образом,

8°А*) = 8 (/(*))¦  (Ю.15)

Произведение линейных преобразований является линейным преобразованием.

Теорема 10.8. Если в некотором базисе линейные преобразования $ и # имеют соответственно матрицы А и В, то их произведение в/ в том же базисе имеет матрицу ВА.

Сумма преобразований. Суммой преобразований / и # некоторого пространства называется преобразование к такое, что для любого вектора х этого пространства

Й(х) = Дх)+#(х).  (10.16)

Сумму преобразований/и # будем обозначать /+§. Очевидно /+8-8 + /-

Теорема 10.9. Если линейные преобразования /и % в некотором базисе имеют соответственно матрицы А и В, то преобразование /+8 в том же базисе имеет матрицу А + В.

Пример 10.5. Даны два линейных преобразования х,' = 7х, + 4х3, х" = х2 — 6х3, х'г = 4х2 -9х3, х2 = Зх[+7Хз,

Х3 = ЗХ, +Х2, Х" = Х^ + Х2 - Х3.

Средствами матричного исчисления найти преобразование, выражающее х", х2, Хз' через х,, х2, х3.

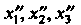
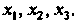
Первое преобразование задано матрицей А, второе - матрицей В, где

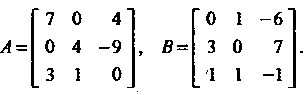
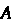
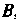
Искомое преобразование в соответствии с теоремой 10.8. имеет матрицу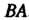 Умножив матрицу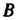На матрицу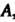, получим

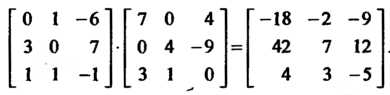
Следовательно, искомое преобразование определяется формулами

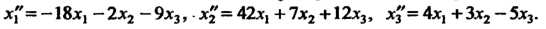
< Предыдущая		Следующая >