10.06. Приведение матрицы линейного преобразования к диагональному виду

 

Теорема 10.6. Матрица линейногопреобразования имеет диагональный вид

Тогда и только тогда, когда каждый базисный вектор является собственным вектором этого преобразования.

Матрица.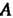Называется приводимой к диагональному виду, если существует невырожденная матрица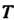Такая, что матрица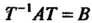Является диагональной. Следовательно, если матрица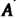Приводима к диагональному виду, то

Где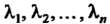- характеристические числа матрицы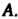

Т е ор е м а 10.7. Матрица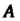Линейногопреобразования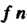-мерного линейного пространства приводима к диагональному виду тогда и только тогда, когда существует базис этого пространства, состоящий из собственных векторов данного преобразования.

Если все собственные числа матрицы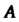Попарно различны, то матрица приводится к диагональному виду.

 

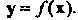
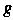
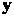
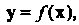
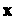
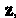
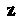
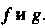
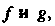
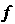
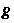
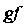
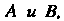
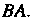
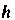
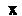
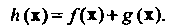
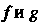
< Предыдущая		Следующая >